Устройство и содержание жд пути - Расчет сдвигов кривой перед выправкой

При текущем содержании пути полного расчета кривых с определением их элементов не делают, да и необходимости в этом нет. Дорожные мастера и другие работники дистанции расчетом определяют лишь направление и величину сдвигов отдельных точек кривой, что облегчает отрихтовку пути в правильное положение.

Рис. 274. Измерение стрел изгиба в кривой

Расчет выполняется по способу разности стрел. Исходными данными для расчета кривых этим способом являются измеренные в натуре через каждые 10 м при 20-м хорде стрелы изгиба рельсовой нити (рис. 274). Ниже приводятся два примера подсчета сдвигов и необходимые пояснения к ним.
Пример первый. Для наглядного представления о состоянии кривой вычерчивают на миллиметровой бумаге график стрел. На графике по горизонтали наносят десятиметровые деления кривой в масштабе 1 : 1 000 (1:2 000), а по вертикали стрелы в масштабе 1 : 1 (рис. 275). Стрелы откладывают во всех точках деления кривой. Если концы ординат (стрел) соединить отрезками прямых, получится ломаная линия. Эта линия называется линией натурных стрел; на рис. 275 она изображена пунктиром.
График помогает ориентироваться в положении круговой и переходных кривых и наметить расчетные величины стрел. При хорошем навыке составление графика стрел для расчета кривой необязательно.
Подсчет сдвигов пути в отдельных точках кривой делают в таблице (табл. 54). В первой графе таблицы записывают номера точек, во второй — измеренные натурные стрелы, в третьей — расчетные стрелы.

Таблица 54
Подсчет сдвигов пути

Расчетными стрелами задаются, но так, чтобы сумма их равнялась сумме натурных стрел. Прежде всего расчетное положение круговой и переходных кривых намечают на графике стрел.

На рис. 275 оно показано линией т — п — р — с, которая называется линией расчетных стрел. Эту линию намечают так, чтобы площади между линиями натурных и расчетных стрел, образующиеся выше и ниже последней (линии расчетных стрел), приблизительно были равновелики.
Надо иметь в виду, что в пределах переходных кривых стрелы постепенно растут по мере приближения к круговой кривой. Поэтому на графике линия стрел переходной кривой (т — п или р — с) занимает наклонное положение.
В пределах круговой кривой одного радиуса величина стрелы не изменяется. Поэтому линия стрел круговой кривой занимает горизонтальное положение (линия п — р).
Установив на графике границы обеих переходных кривых, отмечают в таблице, между какими точками переходные кривые примыкают к Круговой кривой. В рассматриваемом примере переходные кривые примыкают к круговой кривой: первая — между точками 5 и 6, вторая — между точками 15 и 16.
По таблице подсчитывают отдельно суммы натурных стрел в пределах первой переходной кривой, в пределах круговой кривой и в пределах второй переходной кривой. В примере сумма натурных стрел в пределах первой переходной кривой, от точки 1 до точки 5, равна 131 мм; в пределах круговой кривой, от точки 6 до точки 15,— 515 мм; в пределах второй переходной кривой, от точки 16 до точки 20, — 102 мм.
Величины проектных стрел в пределах переходных кривых определяют графически, измеряя в каждой точке расстояния от основания графика до линии расчетных стрел по вертикали.
По рис. 275 находим, что в точках с 1 до 5 и с 16 до 19 стрелы равны следующим величинам (см. табл. 55).

Таблица 55
Величины стрел на переходных кривых  

Для определения средней стрелы в пределах круговой кривой (точки 6—15) сумму измеренных (натурных) стрел делят на число точек круговой кривой. В примере сумма натурных стрел равна 515 мм, число точек равно 10. Следовательно, средняя (расчетная) стрела равна 515 : 10 — 51,5 мм.

Чтобы решить вопрос, в какую же сторону округлить среднюю стрелу, сравним суммы стрел натурных и расчетных в пределах переходных кривых. Сделаем это в таблице (см. табл. 56).

Таблица 56
Сравнение сумм стрел натурных и расчетных

По таблице устанавливаем, что в пределах первой переходной кривой сумма расчетных стрел меньше суммы натурных на 1 мм, а в пределах второй переходной кривой меньше на 6 мм. Поэтому среднюю стрелу круговой кривой целесообразно округлить в большую сторону, т. е. принять ее равной 52 мм.
В таком случае сумма расчетных стрел в пределах круговой кривой (от 6 до 15) будет равна 520 мм, или на 5 мм больше суммы натурных стрел. Общая же сумма расчетных стрел в пределах всей кривой окажется меньше суммы натурных стрел на 2 мм.
Раньше было установлено, что в начале переходной кривой стрела не равна нулю. Поэтому в точках, близко расположенных к началу переходной кривой, желательно стрелу увеличивать на 1—2 мм. Чтобы уравнять суммы натурных и расчетных стрел, в примере целесообразно увеличить на 1 мм стрелы в точках 1 и 19. Это и сделано в табл. 54: в точке 1 стрела увеличена до 5 мм, а в точке 19 до 7 мм.
Установив величины расчетных стрел и уравняв их сумму с суммой натурных стрел, приступают к подсчету сдвигов кривой. В 4-й графе табл. 54 записывают разности стрел, причем принято записывать разность со знаком плюс ( + ), если натурная стрела больше расчетной, и со знаком минус ( — ), если натурная стрела меньше расчетной. Затем разности стрел суммируют алгебраически (с соблюдением правила знаков) и получаемые суммы записывают в 5-й графе таблицы против каждой точки нарастающим итогом.
К разности стрел в нулевой точке, равной нулю, прибавим разность стрел в первой точке, т. е. —3 и полученную сумму —3 запишем в 5-й графе против точки 1. К этой сумме прибавляем разность стрел в точке 2 ( —3) + ( —2) и новую сумму ( —5) запишем в той же графе против точки 2. Затем к —5 прибавим +4 и против точки 3 запишем —1, так как ( —5) + ( +4) = — 1 и т. д.
Сумма разностей стрел в конце 5-й графы должна быть равна нулю, потому что мы уравняли сумму всех расчетных стрел с суммой  всех натурных стрел. Если в 5-й графе нуля не получилось, то нужно найти допущенную ошибку и исправить ее.
Числа, записанные в 5-й графе (сумма разностей стрел), суммируются так же, как суммировались числа 4-й графы. Результаты суммирования записывают в 6-ю графу, а затем их переписывают в 7-ю графу, но на одну строчку ниже. Когда будут приобретены хорошие навыки в суммировании разностей стрел, 6-ю графу из таблицы можно будет исключить, а суммы сумм разностей стрел сразу записывать строчкой ниже.
Числа, записанные в 7-й графе, являются сдвигами, уменьшенными в два раза, или полусдвигами. Чтобы получить полные сдвиги, надо величины, записанные в 7-й графе, умножить на два.
Если путь по полученным сдвигам отрихтовать, то кривая займет правильное положение. Однако до этого необходимо выполнить еще одно обязательное условие расчета кривых. Оно заключается в том, что сдвиг в последней точке расчета должен быть равен нулю. Такое требование вызвано необходимостью сохранить прямой участок пути на прежнем месте, иначе, допустив сдвиг в начале прямой, пришлось бы рихтовать на ту же величину весь прямой участок или исказить его направление.
В нашем примере полусдвиг в последней точке равен 7 мм, его необходимо устранить.
Известно много приемов для ликвидации рихтовки в последней точке расчета. Здесь будет рассмотрен лишь один из этих приемов— графический.
Построение графика несколько задерживает окончание расчета. Но график, о котором пойдет речь, позволяет довольно просто решить и другие задачи, связанные с расчетом выправки кривых. Поэтому учащимся следует с ним познакомиться.
График носит название графика полусдвигов. Построение его несложно. От горизонтальной линии, на которой нанесены десятиметровые деления кривой, откладывают вниз отрицательные полусдвиги, а вверх — положительные. Масштабы для графика полусдвигов принимаются такие же, как и для графика стрел, а именно: горизонтальный (для десятиметровых делений кривой) 1 : 1 000 (1 : 2 000); вертикальный (для полусдвигов) 1 : 1. На рис. 276 приведен график полусдвигов для рассчитываемой кривой.
График полусдвигов удобен тем, что его основание можно изменять — делать его наклонным и даже ломаным. Пользуясь этим, можно с помощью графика решать следующие задачи: приводить к нулю сдвиг в конце кривой; не допускать рихтовки в определенной точке кривой; увеличивать или уменьшать величины сдвигов. Все перечисленные задачи решаются посредством изменения основания графика.
Вычерчивая на графике новое его основание, надо помнить что в тех точках, где основание графика будет иметь угол (перелом) расчетная стрела изменится. Величина, на которую увеличивается или уменьшается расчетная стрела, зависит от величины угла,
Допущенного в оснований графика. Если при новом положении основание между двумя соседними точками кривой поднимется или опустится на 1 мм, то в точке перелома его стрела также изменится на 1 мм. Если же при новом положении основания оно между ближайшими точками поднимется или опустится на 2 мм, то и стрела в точке перелома основания изменится на 2 мм. Новому основанию в конце графика должно быть придано горизонтальное положение. На рис. 277 в точке 5 основанию графика дано иное направление.

Рис. 276. График полусдвигов точек кривой

Рис. 277. Изменение основания графика полусдвигов

При этом новое основание между точками 5 и 6 по отношению к первоначальному его положению поднялось на 1 мм. Между точками 6 и 7 оно поднялось еще на 1 мм. Следовательно, стрела в точке 5 должна быть изменена на 1 мм.
Стрела увеличивается при отклонении основания вверх и уменьшается при обратном его отклонении.
В рассматриваемом примере расчета кривой необходимо ликвидировать полусдвиг, равный 7 мм, в точках 20 и 21. Для этого прежде всего проведем в конце графика полусдвигов горизонтальную линию выше его основания на 7 мм. Такое положение должен занять последний участок нового основания графика (рис. 276).
Затем между горизонтальной линией и первоначальным основанием графика проведем наклонную линию. Чтобы не вносить в принятые стрелы изменения, большие 1 мм, проведем наклонную линию так, чтобы она заняла семь делений кривой, например между точками 12 и 19. Конец наклонной линии не должен находиться дальше точки 19, так как точка 20 находится уже на прямом участке. Если за основание графика принять ломаную линию а — б — в — г, то сдвиг в точках 20 и 21 будет ликвидирован.
Новое основание графика имеет переломы в точках 12 и 19. В точке 12 оно отклоняется вверх (влево), поэтому в этой точке расчетную стрелу надо увеличить на 1 мм, так как между точками 12 и 13 новое основание отклонилось от старого на 1 мм. В точке 19 основание отклоняется вниз (вправо). Следовательно, в точке 19 расчетную стрелу надо на 1 мм уменьшить. Исправленные стрелы записывают в графу 10.
При таком изменении расчетных стрел полусдвиги в точках, начиная с точки 13, уменьшатся на величины, показанные в табл. 57. Эти величины можно получить, измеряя расстояния между старым и новым основаниями графика полусдвигов или вычислением, зная, что если в точке 13 мы отклонили основание на 1 мм и что направление линии дальше до точки 19 не меняли, то в каждой последующей точке, начиная с точки 13, величина отклонения нового основания от старого увеличивается на 1 мм.

Таблица 57
Подсчет полусдвигов при новом основании графика

Измененные полусдвиги записывают в расчетную таблицу (см. графу 8, табл. 54). Имея полусдвиги, нетрудно определить по ним и сами сдвиги, которые в два раза больше полусдвигов. Сдвиги разобранного примера расчета кривой записаны в 9-й графе табл. 54, а в 10-й ее графе — расчетные стрелы, соответствующие сдвигам 9-й графы. На этом расчет заканчивается.
Вернемся к графику полусдвигов (см. рис. 276) и сделаем некоторые выводы, вытекающие из первого примера расчета кривой.

1. Чтобы избежать рихтовки пути в некоторой точке кривой, необходимо и достаточно на графике полусдвигов новое основание провести через эту точку (в примере точки 20 и 21).
2. Для уменьшения сдвигов кривой новое основание графика следует приблизить к линии полусдвигов (в примере точки 14—21).
3. Чем резче изменяется направление основания графика, тем на большую величину изменяется стрела в точке его перелома.
4. Чем больше переломов имеет новое основание графика, тем в большем числе точек кривой будут изменены принятые для расчета стрелы.
5. Новое основание графика за последней точкой кривой должно быть параллельным первоначальному основанию, т. е. горизонтальным.

Пример второй. В данном примере, кроме обычных обязательных условий: уравнивания суммы расчетных стрел с суммой натурных стрел и приведения к нулю сдвига в последней точке кривой, требуется выполнить дополнительное условие — точку 28 сохранить на месте.

Таблица 58
Подсчет сдвигов пути

Измеренные в натуре стрелы записаны в табл. 58, график измеренных стрел изображен на рис. 278. Рассматривая этот график, можно заметить, что кривая имеет два участка, отличающиеся один от другого величиной стрел (радиусов). Поэтому, после того как будет графически намечено положение первой и последней переходных кривых, следует наметить также графически положение каждого участка круговой кривой.
Для первого участка примем расчетную стрелу в 63 мм, а для второго в 42 мм. Между точками 16 и 20 наметим постепенный переход от одной стрелы к другой. Это будет промежуточная переходная кривая, сопрягающая два участка разных радиусов. Расчетные стрелы с графика перенесем в табл. 58 и проверим суммы стрел в пределах каждой части кривой (см. табл. 59).

Таблица 59
Суммы натурных и расчетных стрел

Сумма натурных стрел оказалась на 9 мм больше суммы расчетных стрел. Чтобы уравнять обе суммы, увеличим на 1 мм стрелы в точках с 1 до 5 и с 31 до 34, т. е. в точках первой и последней переходных кривых. Такое изменение стрел не нарушает плавности кривых.
После определения полусдвигов порядком, указанным в первом примере, построим график полусдвигов (рис. 279). Для ликвидации сдвига в точке 35, а также в точке 28 поступим следующим образом. В точках 34 и 35 новому основанию графика дадим горизонтальное положение выше первоначального положения на 25 мм. Этим будет ликвидирован сдвиг в точках 34 и 35. Новое основание графика будем строить от конца к началу графика. В точке 33 отклоним основание от горизонтали книзу на 1 мм, в точке 32 — еще на 2 мм, в точке 31 — дополнительно на 3 мм, в точке 30 — на 4 мм и в точке 29 — на 5 мм, т. е. в каждой точке, начиная с 30 и кончая 34, уменьшим стрелы на 1 мм.
Если основание графика с таким же наклоном продолжить дальше, то оно пересечет линию полусдвигов в точке 28. Между тем для ликвидации сдвига в этой точке и необходимо провести через нее основание. Поэтому продолжим линию основания с таким же наклоном и дальше, тем более, что оно в таком случае пройдет близко от линии полусдвигов и, следовательно, величины сдвигов пути будут небольшими.

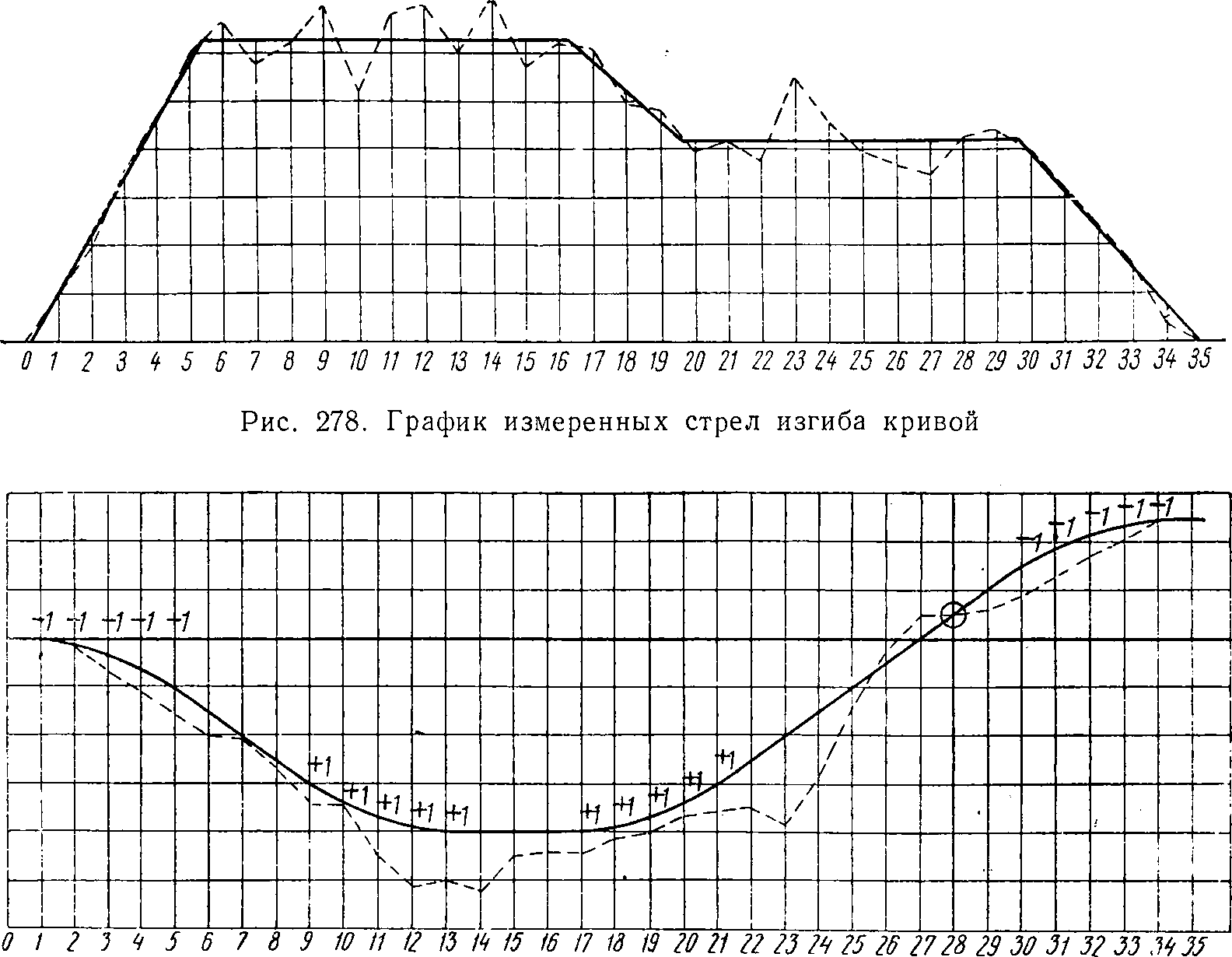
Рис. 279. График полусдвигов точек кривой

В точке 21 остановимся. Дальше вести линию без переломов нельзя, иначе она уйдет далеко вниз. Опустим ее от точки 21 до точки 20 не на 5 мм, а на 4; от точки 20 до точки 19 — на 3 мм, между точками 19 и 18 на 2 мм, между точками 18 и 17 — на 1 мм и дальше проведем линию горизонтально. Допуская такие переломы у основания графика, мы увеличиваем расчетные стрелы на 1 мм в пяти точках: 21, 20, 19, 18 и 17.
Чтобы закончить построение нового основания графика полусдвигов, перейдем к началу графика. В точке 2 опустим основание на 1 мм, в точке 3 — на 3 мм, в точке 4 —· на 6 мм, в точке 5 — на 10 мм и в точке 6 — на 15 мм. Дальше проведем линию, не изменяя ее наклона. Внося новые переломы в основание графика, мы допускаем уменьшение расчетных стрел на 1 мм в точках 2, 3, 4, 5 и 6.
Для постепенного перехода от горизонтального положения к наклонному, при котором линия с каждым делением опускается на 5 мм, потребовалось отступить от первоначального основания графика на 10 мм (см. точку 5, где сделан последний перелом основания). Для обратного перехода к горизонтальному положению, видимо, потребуется также 10 мм (по вертикали). Поэтому, чтобы сомкнуть линию, начатую с начала и с конца графика, проведем новое основание от точки 6 до точки 9 без переломов, в точке 9 остановимся. Здесь основание оказалось на 10 мм выше, чем в точке 17. Следовательно, пора начать переход к горизонтальному положению.

Таблица 60
Подсчет полусдвигов при новом основании графика

В точке 9 делаем перелом и к точке 10 линию опускаем не на 5, а на 4 мм. В последующих точках также делаем переломы, опуская линию в каждой из них на 1 мм меньше, чем в предыдущей. В точке 13 переходим к горизонтальному положению и замыкаем новое основание графика. Допуская переломы линии в точках 9, 10, 11, 12 и 13, мы увеличим расчетные стрелы в этих точках на 1 мм. Отметим это на графике.
Теперь, когда все условия расчета кривой выполнены, можно перейти к его завершению. В отдельную табл. 60 записываем величины уменьшения полусдвигов и по ним определяем полусдвиги при новом основании графика. Затем следует переписать их в табл. 58 и по ним определить величины сдвигов в каждой точке. В графе 10 табл. 58 записаны стрелы, которые соответствуют сдвигам графы 9.
В рассмотренном примере расчета кривой с помощью графика полусдвигов (см. рис. 279) решены следующие задачи:

1. ликвидирован сдвиг в конце кривой;
2. приведен к нулю сдвиг в точке 28;
3. уменьшены сдвиги в большинстве точек кривой.