К каждой эпюре дается также схема разбивки стрелочного перевода (см. рис. 123), на которой указаны все размеры, необходимые для правильной и точной укладки перевода.
На схеме указаны центр стрелочного перевода Ц, представляющий собой точку пересечения осей разветвляющихся путей, положение острия (начала) остряков и математического центра крестовины.
На каждой схеме стрелочного перевода даны расстояния от центра перевода до начала остряков а0 и до математического центра крестовины b0. Сумма этих двух размеров LT называется теоретической длиной перевода. Полной длиной перевода называется расстояние Ln от оси переднего стыка рамных рельсов до заднего стыка крестовины.
За крестовиной иногда укладывают рубки. В этом случае за границу стрелочного перевода принимают второй от крестовины стык рубки. Радиусы переводных кривых невелики. У обыкновенных переводов с крестовинами марки 1/11 радиус переводной кривой имеет величину около 300 м, а с крестовинами марки 1/9 — около 200 м. Поэтому переводные кривые разбивают точно по ординатам. Для прямолинейных обыкновенных стрелочных переводов ординаты даны от рабочей грани полевой рельсовой нити прямого пути до рабочей грани наружной — упорной нити переводной кривой. На симметричных и перекрестных переводах измерение ординат производится по наугольнику от оси симметрии до рабочих граней наружных нитей обеих переводных кривых.
Величины ординат и места, в которых они откладываются, указаны на схемах разбивки стрелочных переводов или в специальных таблицах. Ординаты обычно измеряются через интервалы в 2 м, начиная всегда от точки, расположенной на рабочей грани рамного рельса против корневого зазора остряка. У перевода с кривым остряком переводная кривая начинается от начала остряка и продолжается до переднего стыка крестовины или заканчивается несколько ранее. На схемах укладки стрелочных переводов указаны начало и конец переводной кривой и ее длина.
Рис. 125. Схема разбивки обыкновенного стрелочного перевода
В пределах переводных кривых колея уширяется до 1 536 мм при крестовинах марки 1/11 и до 1 540 мм при крестовинах марки 1/9. Разгонку уширения делают постепенно по внутренней нити кривой. Места и протяжение разгонки уширения колеи также указаны на схемах разбивки переводов.
§ 29. РАЗБИВКА СОЕДИНЕНИЙ И ПЕРЕСЕЧЕНИЙ ПУТЕЙ
Процесс разбивки обыкновенного стрелочного перевода заключается в следующем.
При помощи стальной рулетки или ленты от оси станции отмеряют заданное расстояние по проекту до центра стрелочного перевода (рис. 125) и на оси основного пути закрепляют центр перевода колышком. Затем от этого колышка по оси пути откладывают расстояние а0 — до начала остряков и b0 — до математического центра крестовины.
Закрепив основные точки перевода, откладывают расстояние т от начала остряков до оси стыка рамных рельсов и расстояние q от математического центра крестовины до ее заднего стыка, а также расстояние от математического центра крестовины до ее переднего стыка п.
При укладке стрелочного перевода на существующих путях, когда место укладки крестовины заранее известно, за исходную точку для разбивки перевода берут математический центр крестовины и от него отмеряют по эпюре расстояния, необходимые для определения положения основных точек перевода: начала рамных рельсов, начала остряков и т. д. Все основные точки перевода закрепляют на месте кольями с забитыми сверху гвоздями для точного направления оси пути. На затесанной части кола делают надпись с обозначением точки, например «центр перевода».
Переводную кривую разбивают по ординатам, указанным на эпюрах стрелочных переводов; при этом по ординатам находят положение наружной нити кривой, внутреннюю же рельсовую нить пришивают по шаблону.
Рис. 126. Схема разбивки симметричного стрелочного перевода
Рис. 127. Схема разбивки перекрестного стрелочного перевода
Разбивка симметричного стрелочного перевода несколько отличается от разбивки обыкновенного перевода. Определив положение центра симметричного перевода Ц, провешивают от него ось симметрии I—I (рис. 126). По провешенной оси симметрии от центра перевода откладывают расстояния: а0 до начала остряков, т + а0 до начала рамных рельсов и b0 до математического центра крестовины. Найденные точки закрепляют кольями. Следует запомнить, что у симметричных стрелочных переводов математический центр крестовины находится на оси симметрии. От математического центра откладывают расстояния: q до заднего и n до переднего стыков крестовины, и их расположение также закрепляют кольями.
Разбивка переводных кривых симметричного перевода производится от оси симметрии по ординатам, приведенным на эпюре.
Разбивка перекрестного стрелочного перевода заключается в следующем. Сначала провешивают оси пересекающихся путей I— I и II—II (рис. 127) и находят точку их пересечения Ц, называющуюся центром перевода. Затем провешивают прямую линию Б—Б, которая делит пополам острые углы, образованные пересекающимися осями I—I и II—II.
На прямой Б—Б от точки Ц при помощи стальной рулетки откладывают в обе стороны расстояния, равные
Полученные точки определяют положение математических центров острых крестовин, расстояние между которыми равно А. Далее, под прямым углом к линии Б—Б через точку Ц разбивают линию В—В, на которой откладывают расстояния до математических центров тупых крестовин.
Рис. 128. Закрепление разбивки перекрестного перевода
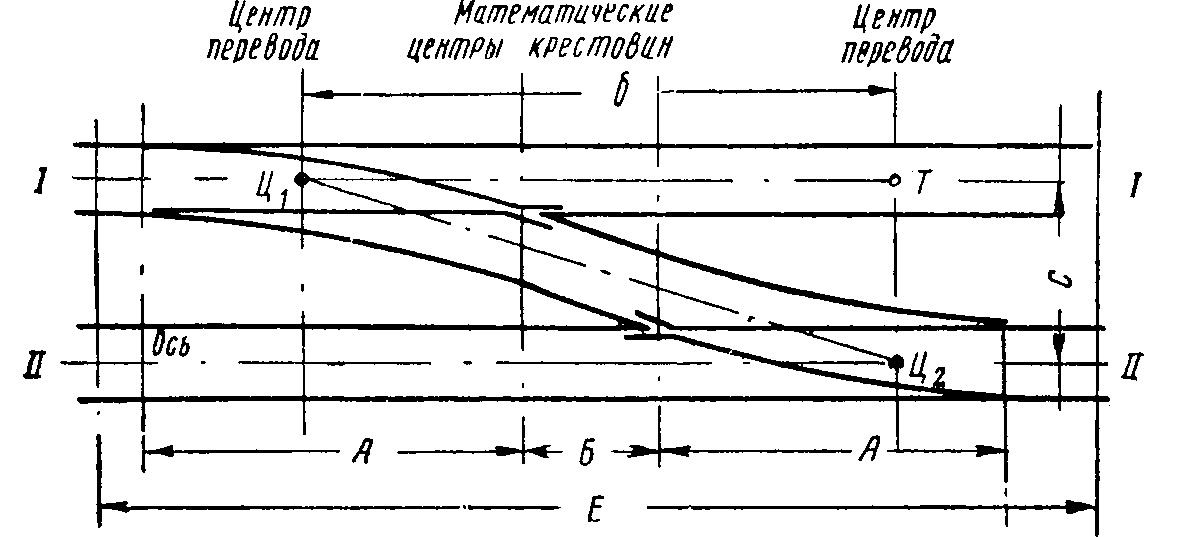
Рис. 129. Схема разбивки съезда между параллельными путями
После закрепления математических центров крестовин перекрестного перевода отыскивают точки, соответствующие передним стыкам рамных рельсов, а затем находят положение остальных частей перевода. Тупые крестовины располагаются на одной прямой с центром перевода. Для проверки и закрепления разбивки против математических центров острых и тупых крестовин устанавливают дощатые обноски, как показано на рис. 128. Натянутые по обноскам шнуры (причалки) должны дать очертание ромба. Точки пересечения шнуров (вершины ромба) должны совпадать с математическими центрами острых и тупых крестовин, а стороны и диагонали ромба точно равняться расчетным расстояниям между центрами тупых и острых крестовин.
Если взять перекрестный стрелочный перевод марки 1/9, то каждая сторона ромба должна быть равна 13 800 мм.
Расстояние между математическими центрами острых крестовин (большая диагональ ромба Б—Б) должно быть равно 27 558 мм.
Расстояние между математическими центрами тупых крестовин (малая ось ромба В—В) равно 1 526 мм.
Разбивка съезда между двумя параллельными путями (рис. 129) производится так.
Сначала находят положение центра перевода на оси первого пути (на чертеже точка Ц1).
Рис. 130. Схема стрелочной улицы под углом крестовины
Затем откладывают по оси первого пути линию Ц1—Т, длина которой определяется умножением расстояния между осями путей на номер (знаменатель марки) крестовины, по формуле б = С х М, (2) где б—расстояние между точками Ц1—Т;
С —ширина междупутья;
М—номер крестовины.
Точка Т расположена против центра другого перевода, который должен быть уложен на втором пути. Вынеся по наугольнику или с помощью геодезического инструмента эту точку на ось второго пути, получим точку Ц2 — центр второго перевода.
От закрепленных на месте центров переводов откладывают по эпюре обыкновенного стрелочного перевода расстояния до всех точек, которыми определяется положение других элементов перевода: начала остряков, рамных рельсов, математического центра крестовины и др.
Рис. 131. Схема сокращенной стрелочной улицы
Стрелочной улицей называется путь, от которого при помощи стрелочных переводов ответвляется в одну сторону
несколько путей. Различают три основных вида стрелочных улиц: улицы прямолинейные нормальные, угол наклона которых равен углу крестовины (рис. 130);
улицы сокращенные, у которых угол наклона больше угла крестовины боковых путей (рис. 131);
улицы веерные, которые в плане представляют ломаные линии и от которых боковые пути отходят в виде веера (рис. 132).
Рассмотрим разбивку стрелочной улицы под углом крестовины.
Для разбивки стрелочной улицы необходимо иметь данные о начале стрелочной улицы, или другими словами, о положении центра стрелочного перевода, которым она ответвляется, и о расстояниях между осями путей, которые отходят от стрелочной улицы.
Сначала в центре стрелочного перевода, которым ответвляется стрелочная улица, откладывают угол крестовины от оси основного пути. Отложив угол и найдя направление Цх—К (см. рис. 130), на котором должна быть расположена стрелочная улица, закрепляют его кольями и шнуром. Затем от оси первого основного пути откладывают расстояния в1, в2, в3, в4 и через найденные точки провешивают направления осей путей параллельно оси первого пути. Продолжая направление путей в сторону стрелочной улицы, находят точки пересечения ее оси с осями параллельных путей (Ц2, Ц3, Ц4). Эти точки являются центрами стрелочных переводов; их нужно основательно закрепить, так как они являются основными для всей дальнейшей работы.
Имея центры стрелочных переводов, направление стрелочной улицы и направление параллельных путей, нетрудно будет разбить, а затем и уложить каждый стрелочный перевод и всю стрелочную улицу.
Вопросы для повторения
- Какое назначение стрелочного перевода?
- Какие разновидности стрелочных переводов применяются?
- Какие основные части имеются в одиночном и двойном перекрестном стрелочных переводах?
- Какие виды корневого крепления остряков применяются и в чем их достоинства и недостатки?
- Что называется шагом остряка и где он измеряется?
- Что называется маркой крестовины и как она определяется?
- Какое назначение контррельсов и как они располагаются относительно крестовины?
- Какие данные содержатся в эпюре стрелочного перевода?
- Что называется центром стрелочного перевода, математическим центром крестовины?
