Графо-аналитические способы расчета
Применяемые в нашей стране аналитические и графо-аналитические способы расчета основаны на работах проф. П. Г. Козийчука, который установил, что сдвиг в η-й точке деления кривой с достаточной точностью может быть принят равным сумме сумм разностей натурных и проектных стрел, взятой от начала кривой до данной точки п,
![]() (15)
(15)
Эта формула позволяет быстро получить искомые сдвижки, если известны проектные стрелы.
Сложность расчета состоит в том, что определить эти проектные стрелы трудно.
У нас в стране широко известны графо-аналитические способы расчета проф. П. Г. Козийчука, инженеров А. Т. Крагеля, В. Д. Поликарпова, М. А. Макурова и других.
Ниже изложен обобщенный графо-аналитический способ расчета выправки железнодорожных кривых, в котором отображены наиболее удачные приемы выполнения отдельных операций, предложенных разными авторами.
В этом способе расчета последовательно выполняют следующие операции.
- По данным натурного замера стрел h строят график стрел прогиба кривой.
- По полученному графику определяют первый вариант проектных стрел.
- Определяют разность (h— Н1) и сумму разностей [Σ(h— Н1)] натурных и проектных стрел, анализ которых позволяет судить, насколько удачно выбраны проектные стрелы.
- Если проектные стрелы выбраны удачно, то подсчитывают сумму сумм разности стрел [ΣΣ(h— Н1)] и строят ее график, по которому корректируют проектные стрелы и определяют сдвиги.
- Выполняют контрольный расчет, который одновременно определяет численные значения окончательных стрел.
Для определения первого варианта значений проектных стрел на графике натурных стрел при помощи прозрачной линейки наносят тонкую горизонтальную линию, соответствующую проектным стрелам на участке круговой кривой. При этом надо стремиться, чтобы алгебраическая сумма площадей, образуемых этой прямой и ломаной линией натурного графика стрел, была близка к нулю. Это примерно будет соответствовать равенству сумм проектных и натурных стрел в пределах круговой кривой. Аналогично наносят тонкие наклонные линии на участках переходных кривых (рис. 21).
Порядок установления величин проектных стрел по построенному графику рассмотрим на конкретном примере.
Пример. На рис. 21 изображен график натурных стрел, приведенных в табл. 10 (все величины в мм). На графике линиями I — I, II— II и III — III обозначено ориентировочное очертание проектного графика стрел.

Рис. 21. График стрел:
1 —1 — проектные стрелы круговой кривой; II-II и /11 —/11 — проектные стрелы переходных кривых; 1 —график натурных стрел; 2 — график стрел после выправки
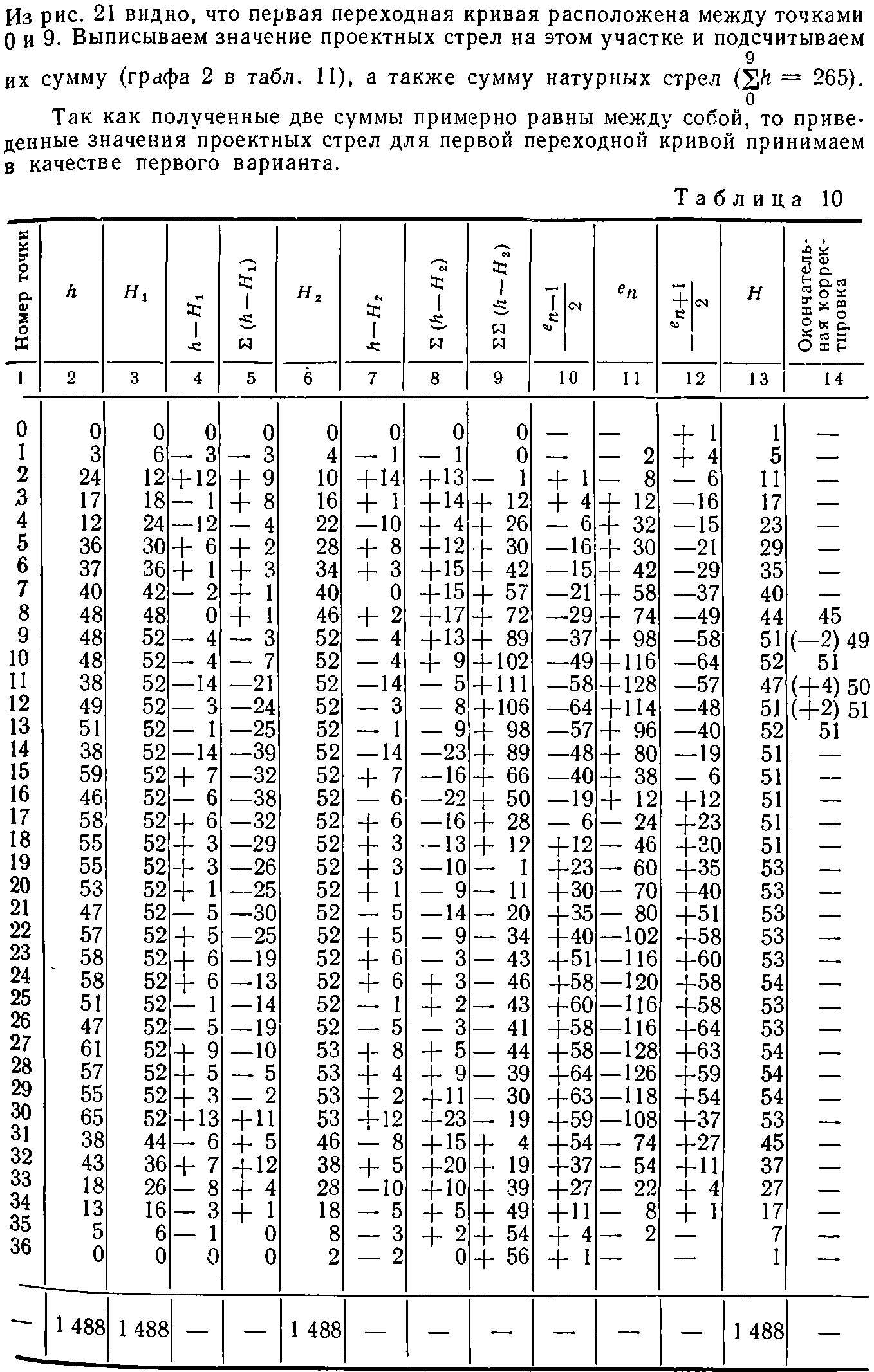



Рис. 22. График суммы разностей стрел:
1 — II вариант новой оси графика; 2 —график суммы разностей стрел; 3—1 вариант Новой оси
После проверки правильности подсчета суммы разностей стрел анализируют полученный результат, чтобы установить, насколько удачно подобраны проектные стрелы. В рассматриваемом примере (см. графу 5 табл. 10) в рядом лежащих точках 9—29 суммы разностей стрел имеют один знак (отрицательный), а многие из них — довольно большую величину (около 40 мм); удвоенные суммы таких однозначных величин [е = 2 ΣΣ(h— Н1), представляющие собой сдвиги, будут иметь большие значения и в конце кривой получится большой сдвиг. Это говорит о неудачном подборе I варианта проектных стрел и о необходимости корректировки их.
Для этой цели строим график (рис. 22) суммы разностей стрел (по данным графы 5 табл. 10), откладывая по оси абсцисс точки деления через 5 мм, а по вертикали — величины сумм разностей стрел в масштабе 1:1. Найденные точки соединяем прямыми линиями. Физический смысл полученного графика 2 состоит в том, что он отображает разность углов поворота натурной и проектной кривых в каждой точке деления. Ось абсцисс можно принять за выпрямленную линию суммы I варианта проектных стрел, тогда кривая графика покажет построенную относительно нее сумму натурных стрел.
Корректируют проектные стрелы нанесением на график новой оси в виде ломаной линии. Отрезки ординат, заключенные между новой осью и кривой графика, представляют собой суммы разностей натурных и новых проектных стрел (откорректированных). На участках кривой, где новая ось параллельна или совпадает с осью абсцисс, проектные стрелы не меняются, а там, где новая ось наклонена вниз или вверх, проектная стрела в каждой точке соответственно уменьшается или увеличивается. Изменение величины стрелы равно величине опускания или подъема оси на расстоянии между двумя точками деления кривой.
Наносим новую ось 3 так, чтобы она как можно чаще пересекала кривую графика, отрезки ординат, заключенные между новой осью и кривой графика, были как можно меньшей величины и чаще меняли свой знак и изломы ее совпадали с точками конца переходной кривой и начала круговой кривой.
Если на протяжении всей переходной кривой или всей круговой кривой новая ось имеет постоянный уклон, то это значит, что во всех точках такого участка стрелы меняются на одну и ту же величину, и техническое состояние проектной кривой не ухудшается. Если же на протяжении круговой кривой новая ось меняет свой уклон, то это значит, что на одной части круговой кривой стрелы изменяются на одну величину, а на другой части — на другую. Последнее нежелательно, так как ведет к образованию составной кривой. На переходных кривых такое явление вообще недопустимо.
Практически наносят несколько вариантов новой оси графика и путем сравнения с учетом местных условий выбирают лучший.
В рассматриваемом примере (см. рис. 22) нанесены два варианта новой оси: первый изображен штриховой линией, второй — сплошной. По первому варианту проектные стрелы на переходных кривых (точки 0—8 и 29—36) остаются без изменений, а на круговой изменяются. В точках 8—15 стрелы уменьшаются на 6 мм, так как здесь линия новой оси наклонена вниз и разность ординат в двух соседних точках равна 6 мм, а в точках 15—29 стрелы увеличиваются на 3 мм. Достоинством этого варианта является то, что новая ось часто пересекает кривую графика, а недостатком то, что излом в пределах круговой кривой ведет к образованию составной кривой с разностью стрел ii — i2 = — θ — ( + 3) = — 9 мм.
По второму варианту новой оси графика сдвиги значительно больше, но зато изломы ее совпадают в основном с границами элементов кривой, благодаря чему техническое состояние кривой не ухудшается. Для дальнейшего расчета принимаем второй вариант.
Измененные проектные стрелы вносим в графу 6 табл. 10, подсчитываем для контроля их сумму, затем подсчитываем и записываем разность натурных и новых проектных стрел (графа 7); суммируем эти величины и записываем суммы их (графа 8) и суммы сумм их (графа 9).
Для точки 1 в графу 9 записываем результат сложения суммы сумм разностей стрел в точке 0, которая равна нулю, и суммы разности стрел в точке 0, равную нулю. Для точки 2 : 0 + ( — 1) = — 1. Затем этот результат ( — 1) суммируем с суммой разности стрел в точке 2 ( + 13) и записываем в точке 3 и т. д.
После подсчета суммы сумм разностей стрел (графа 9 табл. 10) строим график этих величин (график полусдвигов) для окончательной корректировки проектных стрел и определения проектных сдвигов.
Точки деления (рис. 23) наносим на оси абсцисс через 5 мм, так же как и на предыдущем графике. Величины суммы сумм откладываем в масштабе 1:1. Физически этот график представляет собой утрированный план линии. Горизонтальную ось графика можно представить, как выпрямленную проектную кривую, характеризуемую откорректированными проектными стрелами, приведенными в графе 6 табл. 10, а ломаную линию графика abcde —- как план натурной кривой, начерченный относительно выпрямленной проектной кривой.
О необходимости вторичной корректировки проектных стрел говорит то, что в конечной точке кривой (точка 36) сдвиг не равен нулю (е36 = 2 * 56 = = 112 мм), а это недопустимо. В других случаях причиной корректировки могут быть излишне большие сдвиги на отдельных участках или направленность их в сторону, в которую по местным условиям нельзя рихтовать, и т. п.
Окончательно корректируют проектные стрелы нанесением на графике полусдвигов новой оси при помощи линейки и параболических лекал, ординаты которых у определяются уравнением
![]() (18)
(18)
где х — номер точки деления.
Отрезки ординат, заключенные между проводимой осью и существующей кривой графика, представляют полусдвиги, соответствующие новым проектным стрелам; при этом на участках новой оси, очерченных параболой, стрелы изменяются на величину Δ//, а на участках, очерченных прямой линией (горизонтальной или наклонной), проектные стрелы не изменяются.
Лекала изготовляют из прозрачного материала по ординатам, подсчитанным по формуле (18). Практически достаточно иметь два лекала, построенных при Δ// = 1 мм и Δ// = 2 мм.
При нанесении новой оси графика полусдвигов лекало необходимо располагать так, чтобы вертикальная и горизонтальная оси были параллельны соответствующим осям графика полусдвигов.
Новая ось должна быть сопряжена по касательной с осью абсцисс в начале кривой и в конце с горизонтальной линией, проходящей через последнюю точку кривой графика полусдвигов. Криволинейные участки новой оси, наносимые при помощи лекал, должны сопрягаться между собой и с прямолинейными участками также по касательным.

Рис. 23. График полусдвигов
Новая ось должна как можно чаще пересекать кривую графика, чтобы сдвиги имели наименьшее значение и чаще менялись по знаку. Следует в основном обходиться лекалом, построенным с Δ//-— 1 мм, и только в необходимых случаях применять лекало, построенное при Δ// = 2 мм. В точках деления, которые не должны смещаться (переезды, мосты и т. д.), сдвиги должны быть равны нулю; для этого новая ось в этих точках должна пересекать кривую графика. Если сдвиги на отдельных участках должны быть определенного знака или величины, то это необходимо учитывать при проведении новой оси.
После нанесения новой проектной оси замеряют отрезки между ею и кривой графика, записывают их в графу 11 сдвигов расчетной таблицы (см. табл. 10) и выполняют контрольный расчет. На этом расчет кривой заканчивают.
В графике abcde полусдвигов (см. рис. 23) ординаты полусдвигов намечены не точками, как это делают обычно, а горизонтальными штрихами длиной 4—5 мм, позволяющими более точно отсчитывать ординаты (между новой осью и кривой графика). Криволинейные участки новой оси очерчены лекалом, построенным при ΔH = 1 мм. Для максимального приближения новой оси к кривой графика отклонение ее от оси абсцисс начато с точки 0, в которой лекало располагают так, чтобы вершина параболы совпала с точкой 0 (положение I лекала); после этого лекало обводят карандашом тонкой линией of. Чтобы в конце кривой сдвиг был равен нулю, новая ось должна быть сопряжена с горизонтальной линией, проходящей через последнюю точку кривой графика (точка е). Для этой цели располагают лекало в положении, обозначенном цифрой II и наносят линию eg. Сопряжение двух парабол может быть сделано прямой ое или двумя параболами, соответствующими положениям /// и IV лекала. В первом случае на большом протяжении кривой (где новая ось очерчена прямой линией) проектные стрелы не изменяются, но сдвиги, равные удвоенному расстоянию между новой осью и кривой графика, в некоторых точках остаются очень большими.
При сопряжении кривых of и eg двумя параболами проектные стрелы в первой части кривой уменьшаются на 1 мм в каждой точке, а во второй части увеличиваются на такую же величину, но сдвиги будут значительно меньше. Поэтому принимаем сопряжение по параболам. Новая ось имеет очертание линии okle.
Чтобы еще более уменьшить сдвиги в рассматриваемом примере, можно новую ось еще более приблизить к кривой графика, как это показано на рис. 23 штриховой линией; в этом случае кривые новой оси очерчивают по лекалу, построенному при ΔH =2 мм, и тогда стрелы на одной части кривой уменьшатся на 2 мм, а на другой — увеличатся на 2 мм. В результате кривая будет составной с разницей в стрелах 4 мм. Такой вариант принять нельзя.
На новой оси принятого варианта наносим горизонтальные штрихи против каждой точки деления кривой в соответствии с ординатами параболы, намеченными на лекале.
Замеренные расстояния между штрихами на новой оси и кривой графика полусдвигов удваиваем и записываем в графу 11 табл. 10, а в соседних точках записываем в графы 10 и 12 полусдвиги с обратным знаком. Суммируя по каждой точке величины, записанные в графах 2, 10, 11, 12, получаем проектные значения стрел, которые записываем в графе 13.
Анализ величин графы 13 позволяет видеть, не допущены ли в расчете ошибки. О последнем свидетельствуют резкие колебания в стрелах круговой кривой или нарушение установленной закономерности роста стрел переходных кривых. Незначительные колебания (например, 3—4 мм) могут быть устранены корректировкой, произведенной в графе 14 табл. 10. В скобках указаны величины дополнительных сдвигов, а цифрами — откорректированные стрелы. Но величины дополнительных сдвигов исправляют проектные сдвиги. Значительные колебания стрел свидетельствуют о том, что в расчете допущена ошибка, которую необходимо найти и исправить.
