Задачи распределения пассажиропотоков на ТС связаны с поиском кратчайших путей между центрами транспортного тяготения методами теории графов.
Графом G (R, U) транспортной сети называют совокупность ее узлов R и соединяющих их дуг U. За Вершины графа принимают центры транспортных районов и других объектов массового тяготения населения, а дугами изображают участки улично-дорожной сети, пути пешеходного подхода к остановочным пунктам МПТ и ИПТ, не связанные с улично-дорожной сетью участки внеуличных городских путей сообщения, а также пересадки с одного вида ГПТ на другой. Дуги, допускающие движение только в одном направлении, называют ориентированными, а граф, состоящий из таких дуг, — ориентированным графом. Дуги, допускающие движение в обоих направлениях, называют неориентированными, а составленный из них граф — неориентированным. В общем случае ТС включает в себя и ориентированные, и неориентированные дуги. Такой граф называют смешанным. Совокупность путей, связывающих вершину (узел) R со всеми остальными, называют деревом графа.
Для поиска кратчайших путей на заданном графе G (R, U) используют итерационные алгоритмы поэтапного наращивания и коррекции дерева кратчайших путей, найденного на предыдущей итерации. Предложен рад таких алгоритмов — алгоритмы Минти, Мура, Форда-Фалькерсона и др. В алгоритме Минти и его модификациях дерево кратчайших путей находят методом последовательного наращивания. На каждой последующей итерации к части дерева кратчайших путей, полученного на предыдущей итерации, добавляется одна дуга, т. е. находят кратчайший путь до очередной вершины. Построенная на начальных итерациях часть дерева кратчайших путей на последующих итерациях не меняется. Задача решается за R—1 итерацию. Алгоритм позволяет находить кратчайшие пути от заданной вершины до всех остальных или только части вершин графа.
Более эффективны, однако, алгоритмы Форда-Фалькерсона, Мура и др., в которых построенные деревья могут многократно корректироваться на последующих итерациях. Все они основаны на методе потенциалов. Исходной вершине, к которой находят кратчайшие пути из всех остальных вершин графа, присваивают потенциал П=0, остальным — некоторый заведомо большой потенциал М. Потенциал может численно определять расстояние корреспонденции между рассматриваемыми вершинами i и j, время сообщения между ними при движении пешком или на рассматриваемом виде транспорта, стоимость проезда или другую характеристику а ветви между вершинами i и j. Задача заключается в «просмотре» всех вершин графа с целью понижения потенциалов соседствующих и считается оконченной, когда все вершины графа получают минимальные потенциалы.

В результате просмотра вершин на каждой итерации потенциалы части вершин графа понижаются. Итерационный процесс продолжается до тех пор, пока на графе не останется ни одной вершины, потенциал которой можно понизить. Полученные в результате этого процесса потенциалы вершин представляют собой минимальные потенциалы относительно центра построения (начальной вершины), т. е. кратчайшие расстояния от нее, минимальные затраты времени на передвижение и т. д.
Итерационные алгоритмы различаются порядком просмотра вершин, который определяет затраты времени на решение задачи. Вершины просматривают в порядке возрастания или убывания их номеров (алгоритмы Форда-Фалькерсона) или попеременно в порядке возрастания и убывания (алгоритм «метла», разработанный Институтом кибернетики АН УССР). При машинной реализации более эффективными по критерию затрат времени на решение задачи являются алгоритмы попеременного просмотра вершин.
В качестве примера рассмотрим поиск кратчайших путей на графе рис. 11.10, а методом Форда. За исходную вершину графа, по отношению к которой определяются кратчайшие пути из остальных вершин, примем узел 7, за потенциалы а ветвей — расстояния между соответствующими узлами, показанные цифрами над ветвями.
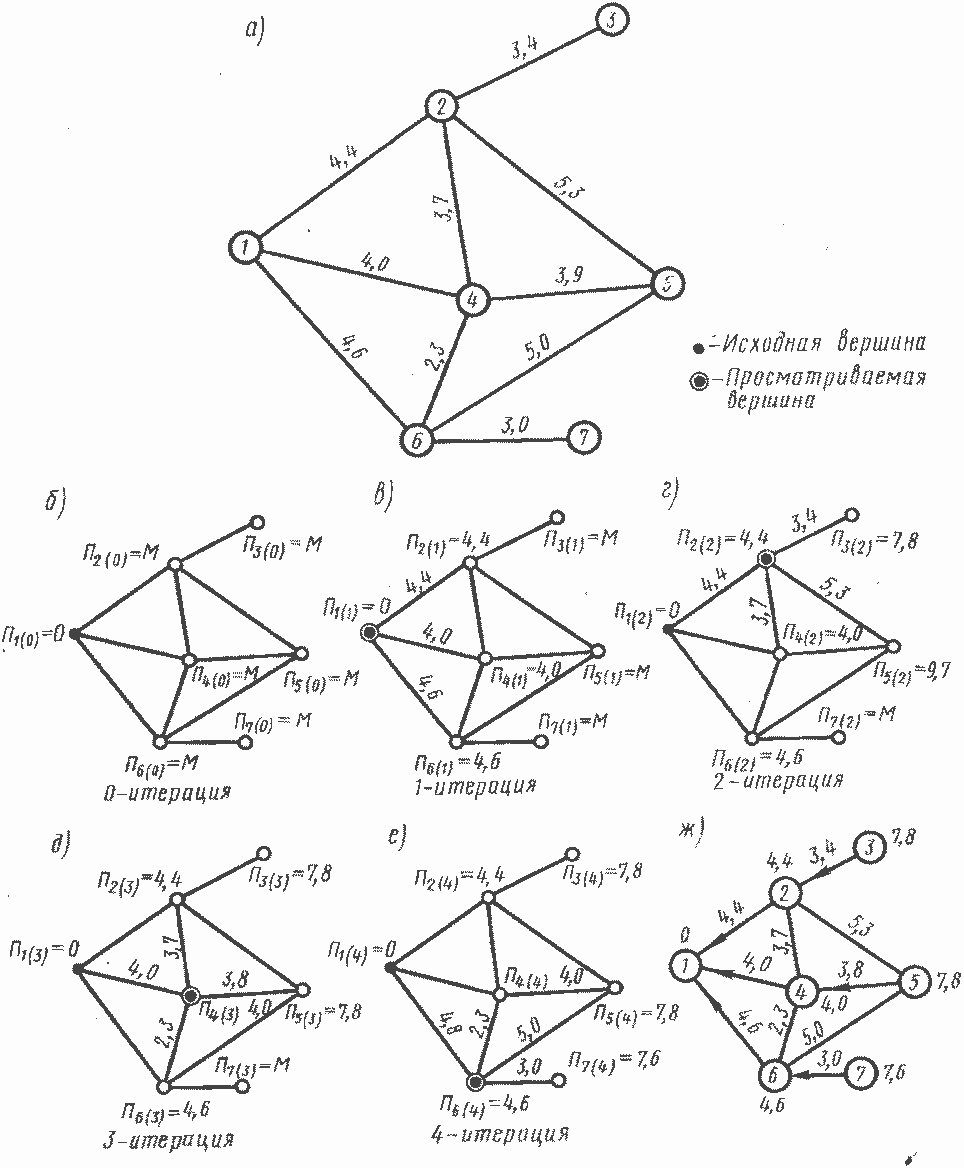
Рис. 11.10
Итерации поиска кратчайших путей на графе ТС методом потенциалов:
а — исходный граф; б—е — итерации поиска кратчайших путей до вершины; ж — конечный граф кратчайших путей
Для уменьшения объема вычислений операции поиска потенциалов будем проводить вначале для узлов, смежных с исходной вершиной 1, а затем для узлов, смежных с рассмотренными ранее.


