Трамвайные узлы представляют собой сочетание стрелочных переводов, пересечений и соединяющих их участков пути. При проектировании узлов следует исходить из желательности применения типовых эпюр стрелочных переводов и пересечений, целесообразности наименьшей протяженности узлов в целом, необходимости обеспечить достаточно плавное движение с необходимыми скоростями. Лишь в порядке исключения допускается использование нетиповых эпюр и нестандартных радиусов кривых.
Подбор эпюр выполняется графически на плане трассы исходя из условий планировки, габаритных расстояний, а также из заданной величины угла поворота и радиуса круговой кривой. Собственно расчет заключается в построении расчетных схем и определении необходимых для проектирования элементов узла. Часть параметров при этом принимается на основании действующих нормативов, часть определяется расчетом. В ходе проектирования все элементы узла должны быть геометрически взаимоувязаны.
При расчете узла из одиночного стрелочного перевода и застрелочной кривой (рис. 104) считаются данными или принимаются на плане трассы по местным планировочным условиям значения: Упл — угол поворота линии и R — радиус круговой кривой. Кроме того, из подобранной для этого случая эпюры стрелочного перевода принимаются его элементы: Rс — радиус стрелки; Rк — радиус крестовины и переводной кривой; tс — тангенс стрелочного перевода со стороны стрелки; tк — тангенс стрелочного перевода со стороны крестовины; Уп — угол поворота перевода.
Определяем угол поворота круговой кривой
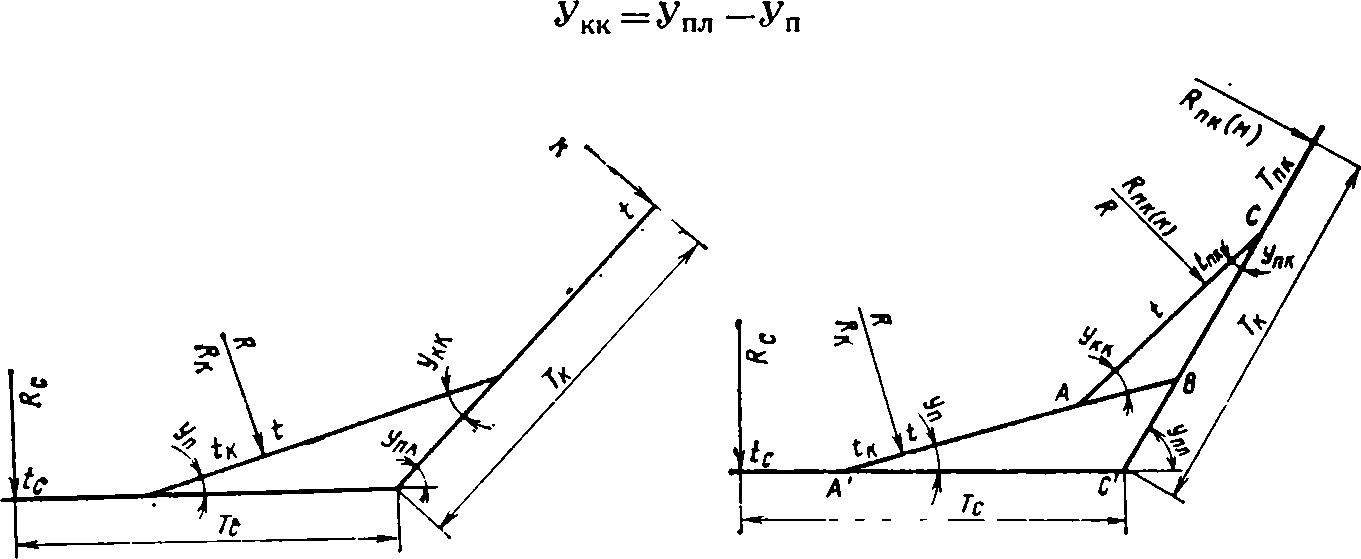
Рис. 104. Расчетная схема узла из одиночного стрелочного перевода и застрелочной кривой
Рис. 105. Расчетная схема узла из одиночного стрелочного перевода с переходной кривой

Расчет двухколейного ответвления (рис. 106, а) сводится к последовательному решению одиночного стрелочного перевода и одноколейного ответвления, а также определению забегов между началами стрелок и кривых, позволяющих увеличить ширину междупутья.
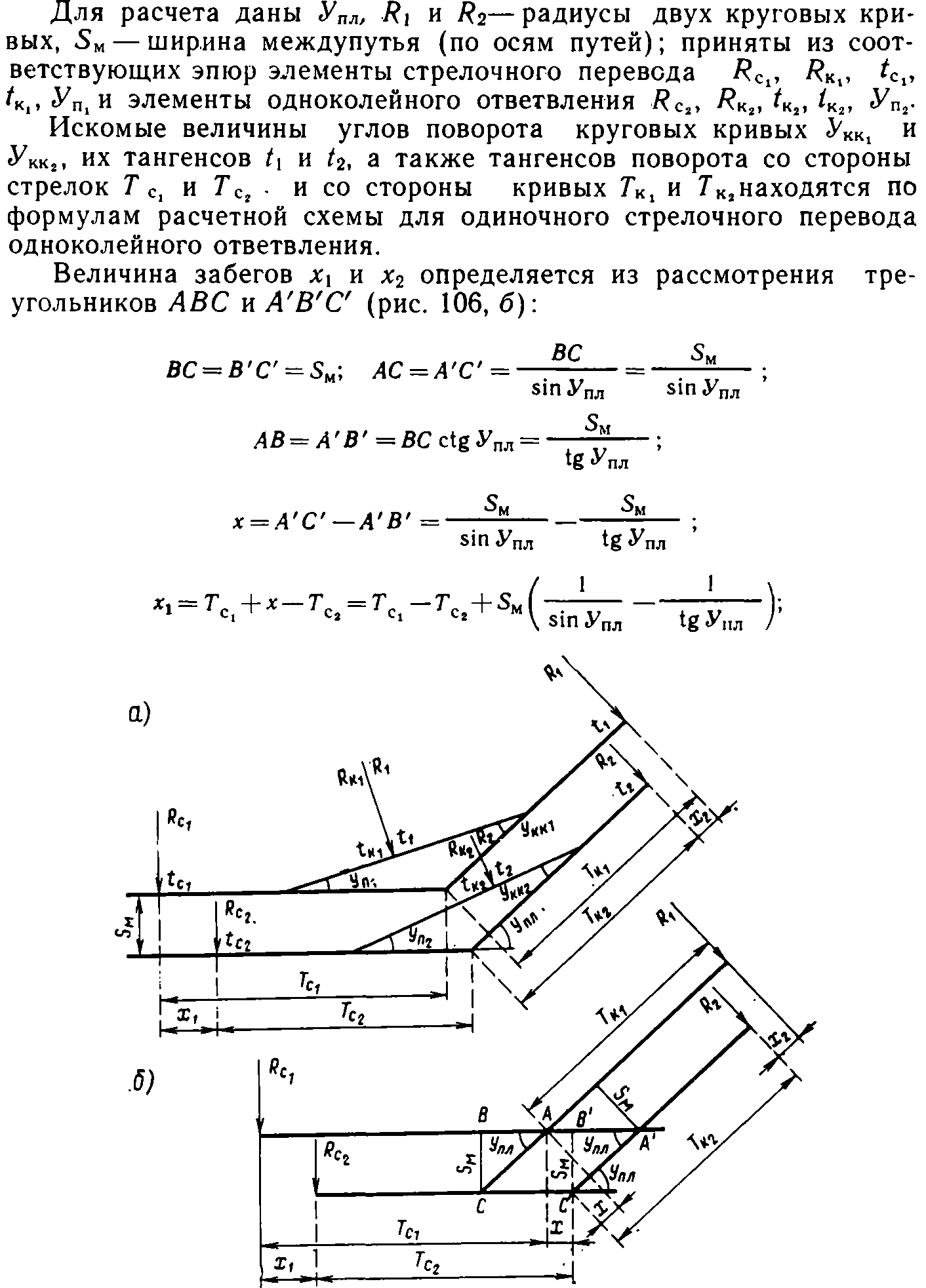
Рис. 106. Расчетная схема двухколейного ответвления: а — общий расчет; б — расчет забегов
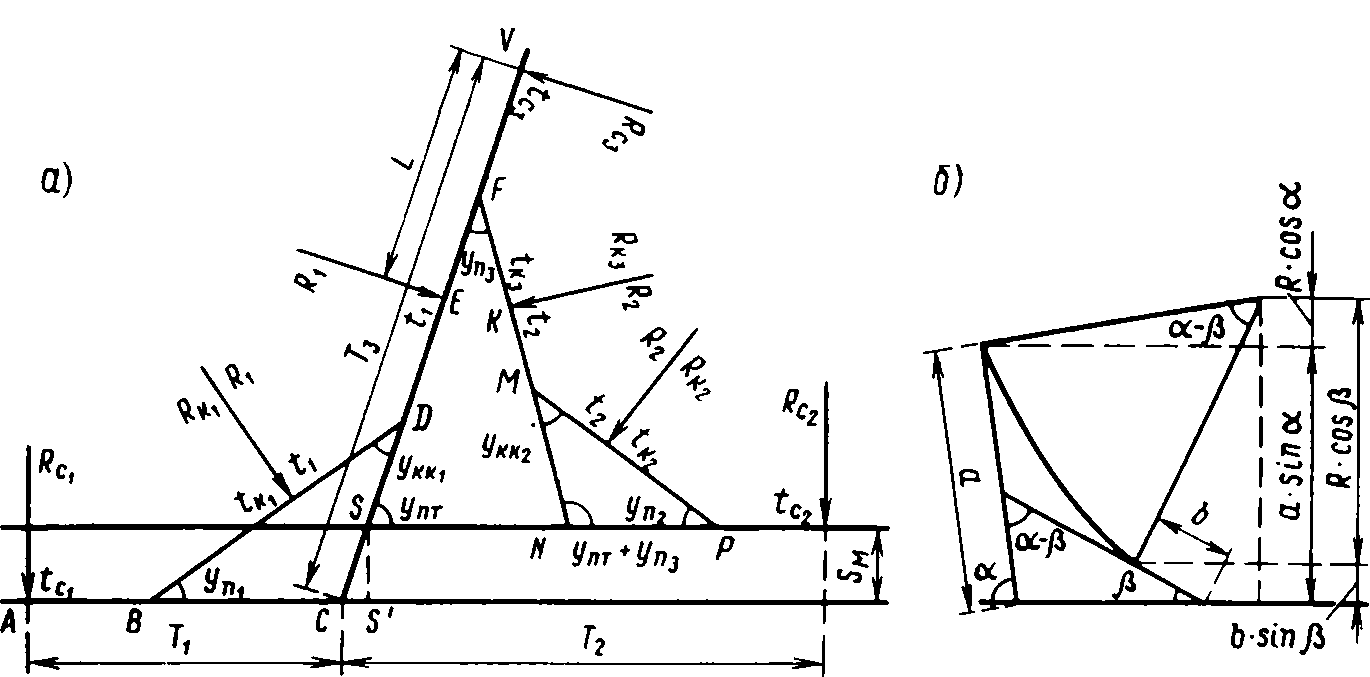
Рис. 107. Расчетная схема одноколейного треугольника: а — общий расчет; б — расчет промежуточной кривой

Для дальнейшего расчета рассмотрим отдельные треугольники на расчетной схеме.


Двухколейный треугольник (рис. 108) при расчете рассматривается как три двухколейных ответвления, соединяемые при трассировке прямыми и кривыми участками пути. При углах поворота от 80 до 100° может оказаться целесообразным применение симметричного варианта для одного из двухколейных ответвлений. Треугольник становится симметричным при угле поворота, равном 90° — такое решение является наиболее простым, так как при проектировании достаточно рассчитать лишь одну его половину.
При расчете двухколейного треугольника заданными считаются Упт (угол поворота треугольника) и Sш (ширина междупутья), по типовым эпюрам выбираются элементы трех одиночных стрелочных переводов и трех одноколейных ответвлений.

Рис. 108. Расчетная схема двухколейного треугольника
Можно предварительно решить два двухколейных ответвления, соединенных между собой кривыми (по местным условиям при этом выбираются радиусы круговых кривых R1 и R2). После этого решается третье двухколейное ответвление, конец круговой кривой в котором совпадает с концом прямого направления пересечения. Возможен вариант, при котором по выбранным R1, R3 и R4 решается R2. Во всех случаях искомыми являются элементы соединительных кривых и большие тангенсы треугольника.
После выполнения расчета элементов узлов надо выполнить их построение на плане трассы. Это построение должно выполняться в определенной последовательности. Рассмотрим эту последовательность на примере двухколейного ответвления
На базисе, которым служит выполненный в осях план двухпутного участка трассы, вначале на том пути, который является внутренним относительно проектируемого поворота, намечается точка О — центр поворота ответвления, от нее под углом поворота линии Упл откладывается направление тангенса со стороны кривой. Потом на базисном направлении влево от вершины угла Упл откладывается длина Полученная точка А есть начало одиночного перевода. Вправо от нее откладывается длина тангенса стрелочного перевода со стороны стрелки tc Вновь полученная точка В есть центр стрелочного перевода, от нее под углом УП1 откладывается направление тангенса стрелочного перевода со стороны крестовины и его длина tК1, а затем и длина тангенса круговой кривой t1. Точка С, где заканчивается должна совпасть с направлением, исходящим из точки О под углом Упл. Это вершина круговой кривой CD. Остается отложить второй тангенс той же кривой CD. Отрезок OD должен по длине совпасть с откладываемой от точки О длиной тангенса поворота со стороны кривой ТК1. В этом проверка правильности построения.
Затем строится стрелочный перевод с пересечением. Вначале на втором (наружном) базисном пути от проекции на него точки А (A") надо отложить забег x1 и затем от полученной точки А" отложить по тому же направлению длину тангенса поворота со стороны стрелки TС2. Полученная точка О' есть центр поворота второго ответвления (с пересечением). От нее под углом поворота линии Упл откладывается также направление тангенса поворота со стороны кривой Тк2. Затем от точки А" (начало второго стрелочного перевода) вправо откладывается А'В'— величина tc2 и из точки В' под углом Уп2 — направление тангенса стрелочного перевода до пересечения в точке С' с линией, проведенной из точки О'. На В'С' следует отложить длины /к2 и /2. Совпадение суммы этих длин с длиной отрезка В'С' — вторая проверка правильности построения. Далее от вершины кривой С' следует отложить длину второго тангенса t2 до точки D'. Расстояние от D' до D" (проекция D на ось второго пути) должно быть равно Х2 — это третья проверка правильности расчета и построения.
Если одна из проверок показывает несовпадение, следует внимательно проверить расчеты и построения и при необходимости уменьшить радиус второй кривой, сместить вправо точку О' с учетом необходимого уширения междупутья в кривой, а иногда и подобрать другую эпюру стрелочного перевода.
