Глава VI
РАСЧЕТЫ ПУТИ НА ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ
РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ. ОСНОВЫ СТАТИЧЕСКОГО РАСЧЕТА РЕЛЬСА
Расчеты рельсового пути на прочность заключаются в определении напряжений, возникающих в элементах пути под влиянием вертикальных нагрузок от движущегося подвижного состава, и сравнении этих напряжений с допускаемыми. На основе этого сравнения выполняется выбор таких параметров (размеров, количества, прочности) элементов пути, которые обеспечивают надежность и долговечность всей конструкции.
Все многообразие путевых конструкций можно разделить на две группы: пути на упругих основаниях, распространяющие давление от рельсов только в поперечном направлении, т. е. с нулевой продольной жесткостью, и пути на жестких основаниях, распределяющих давление и поперек пути и вдоль пути, т. е. обладающих и поперечной и продольной жесткостью. Обычные рельсошпальные конструкции относятся к первой группе.
На путь в процессе его взаимодействия с движущимися вагонами или локомотивами действуют, кроме нагрузки от колеса, различные дополнительные вертикальные и горизонтальные силы. Характер их действия, как уже говорилось, зависит не только от величины самой нагрузки, но и от целого ряда эксплуатационных особенностей пути, подвижного состава, условий их содержания. Однако расчеты рельсовой нити на прочность ведутся только по вертикальным силам, действующим на рельс центрально, в плоскости симметрии. Рельсы обеих нигей при этом считаются равнозагруженными. Для учета действия горизонтальных поперечных сил, а также внецентренности приложения вертикальных из-за наличия подуклонки расчетные напряжения в подошве рельса умножаются на некоторый экспериментально определенный коэффициент. Значения этого коэффициента возрастают по мере увеличения радиусов кривой, скоростей движения и уменьшаются с повышением мощности рельса. Они всегда больше единицы. Непосредственно рассчитываются лишь горизонтальные воздействия на наружный рельс в кривой и напряжения, возникающие от продольных горизонтальных сил при изменениях температуры.
При расчете элементов пути вводится еще ряд допущений. Так, рельс принимается за неразрезную балку бесконечно большой длины, неизменного сечения, лежащую, на сплошном равноупругом основании (механический стык при этом рассчитывается отдельно). Собственный вес путевой решетки не учитывается в расчете, так как его влияние на величину напряжений в элементах пути крайне незначительно. Считается далее, что между удельным давлением на основание шпалы и его упругой просадкой существует линейная зависимость; что движущиеся колеса нигде не отрываются от головки рельса и не создают ударных воздействий; что балласт сопротивляется прогибу путевой решетки не только вниз, но и вверх. Эти допущения незначительно влияют на точность расчетов, но зато дают возможность проводить их по достаточно строгим формулам теории упругости.
При расчетах пути на прочность необходимо установить его основные расчетные характеристики. К ним относятся коэффициент постели шпалы (коэффициент податливости основания) С, модуль упругости подрельсового основания U, коэффициент относительной жесткости рельса и его основания К, коэффициент относительной жесткости шпалы и ее основания K1, а также коэффициент изгиба шпалы а. В расчетных формулах фигурируют также знакомые нам момент инерции I и момент сопротивления W.
Коэффициент С характеризует упругие свойства балласта под шпалой. Его можно рассматривать как силу, приходящуюся на 1 см2 площади основания шпалы и вызывающую ее осадку на 1 см:
С=Р/у,
где Р — давление, МПа (кгс/см2); у — упругая осадка шпалы, см.
Модуль упругости U характеризует упругие свойства подрельсового основания в целом. Это величина, равная распределенной нагрузке, приходящейся на 1 см длины рельса, которая вызывает осадку рельса на 1 см. Модуль упругости, МПа (кгс/см2),
![]()
где а — коэффициент изгиба шпалы (отношение средней осадки основания к осадке в подрельсовом сечении); а и b — длина и ширина шпалы, см; I — расстояние между осями шпал, см.
Значения коэффициентов относительной жесткости К и K1 становятся ясны в ходе самого расчета.
Следует отметить, что закон Гука, распространяющийся на упругие тела, не бесспорен в отношении грунтов. Грунт практически не работает на растяжение. Для него характерны значительные остаточные деформации, которые в ряде случаев даже превышают упругие. Поэтому правильнее говорить не о модуле упругости, а о модуле деформации.
Численные значения основных расчетных характеристик для новых рельсов приведены в табл. 36. При выполнении практических расчетов для их определения необходимо подсчитать момент инерции для рельсов с соответствующим износом.
Таблица 36. Основные расчетные характеристики пути
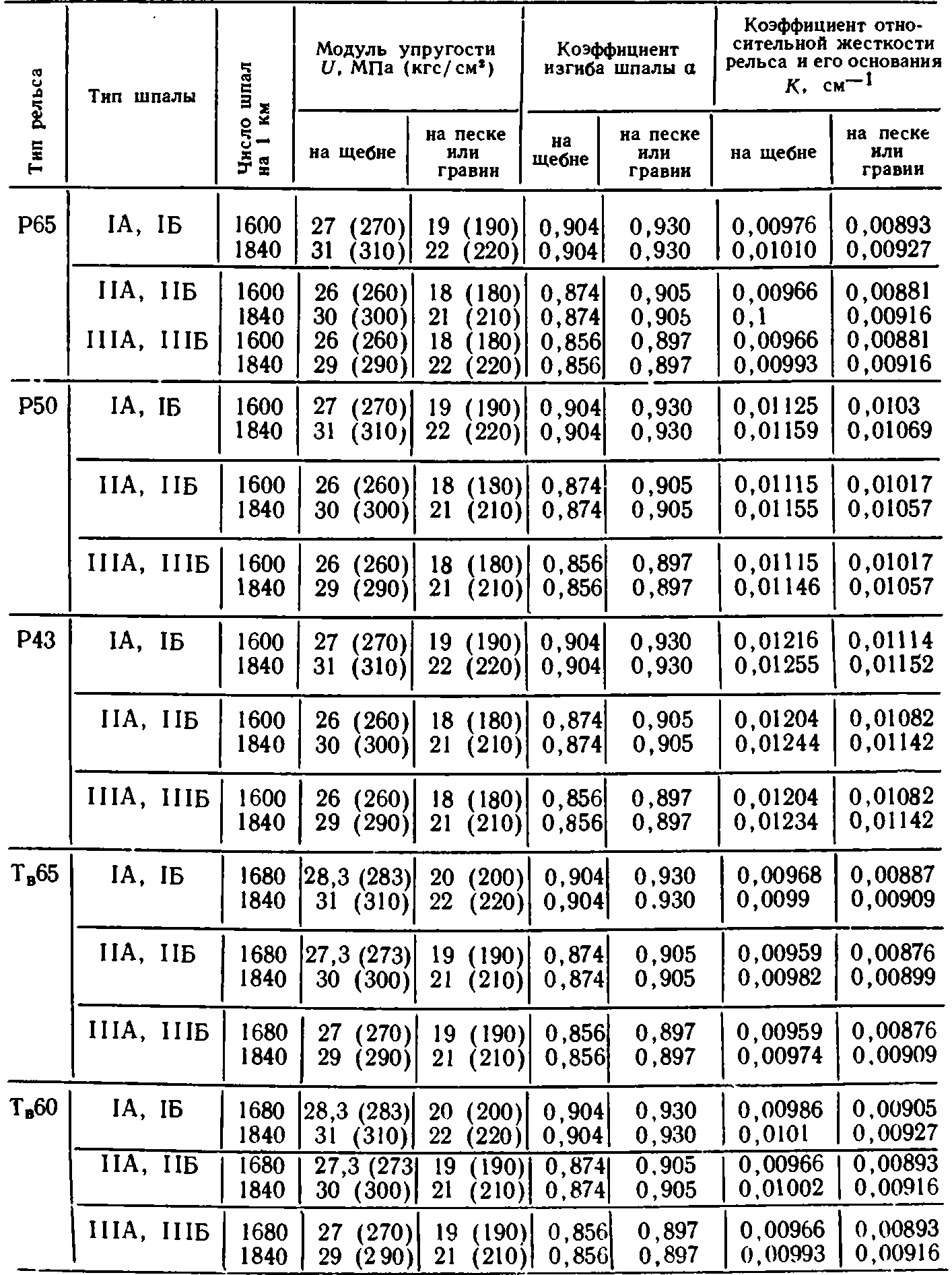
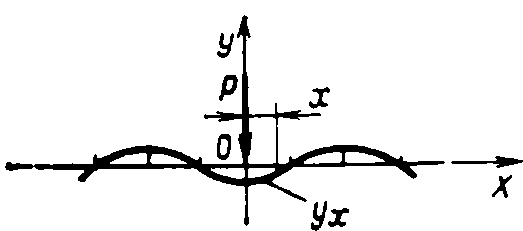
Рис. 86. Схема статического расчета рельса на прочность
Из табл. 36 видно, что значения модуля упругости U для пути на деревянных шпалах в зависимости от их типа и эпюры меняются сравнительно в небольших пределах (до 19%) и лишь переход к более тяжелому балласту заметно увеличивает диапазон возможных изменений U (до 42%). Установлено значительное увеличение жесткости пути при переходе балласта в замороженное состояние. Модуль упругости на деревянных шпалах достигает при этом 80—90 МПа (800— 900 кгс/см2). Особенно ощутимо меняется жесткость пути при укладке железобетонных шпал. На щебеночном балласте в этом случае U достигает 200 МПа (2000 кгс/см2). Очевидно, что на величину модуля деформации (модуля упругости) подрельсового основания влияет степень уплотнения балласта. Все данные, приведенные в табл. 36, относятся к исправному, прошедшему длительную обкатку пути.
Если на рельс, который мы условились принимать за балку, лежащую на сплошном упругом основании, в некоторой точке О действует одиночная сосредоточенная нагрузка Р (рис. 86), то для расчета этой балки можно применять формулы, известные из курса «Сопротивление материалов».
Изгибающий момент в балке равен второй производной функции ординат изогнутой оси балки, умноженной на жесткость балки, т. е. на произведение модуля упругости материала Е (для рельсовой стали Е=2,1x105 МПа = 2,1x106 кгс/см2) и момента инерции ее сечения 1 см,

Проинтегрировав основное дифференциальное уравнение расчета по очевидным граничным условиям (при![]() _ при
_ при

Быстрое убывание ординат μ и η позволяет принимать во внимание влияние только трех соседних осей. Причем в некоторых случаях соседние оси могут не увеличивать, а уменьшать расчетную нагрузку, как бы разгружая рельс.
