При решении задачи методом перемещений на все узлы расчетной схемы накладываются связи. Процедуре выполнения блочной итерации для узла i соответствует освобождение его от связей, в результате чего он перемещается в равновесное положение. Затем на него вновь накладываются связи и выполняются итерации для других узлов. Если после выполнения итераций для узлов, связанных конечными элементами с узлом i, освободить его от связей, то он сместится к новому равновесному положению, так как соседние с ним узлы переместились. Но в связи с тем, что связи не снимаются до выполнения для него итерации на следующей прогонке, в них возникают реакции, которые в вычислительной процедуре трактуются как невязки. Самую высокую скорость сходимости решения обеспечивает такой порядок обхода узлов, когда итерации в первую очередь выполняются для узлов с наибольшими невязками. Действительно, на первой прогонке невязка имеет наибольшую величину для узла i и равна внешней силе Рi (рис. 7.8). Для остальных узлов невязки равны нулю. Если обход начать с узла j, ряд вычислительных операций будет выполнен впустую. При нулевых невязках положения узлов не будут меняться.

Рис. 7.8. Конечно-элементная схема контактирующих тел: А, П — активная и пассивная контактные поверхности; а, b- контактные узлы
И лишь после выполнения итерации для узла i невязки для ближайших к нему узлов не будут нулевыми. На следующей прогонке невязки для узлов будут отличны от нуля, однако, порядок, в котором обходятся узлы, окажет влияние на скорость сходимости решения.
В программной реализации метода строится массив номеров узлов, расположенных в порядке их обхода. В начале массива стоят узлы с заданными в виде перемещений или сосредоточенных сил внешними нагрузками. Для включения следующих за ними номеров рассматриваются конечные элементы, прилегающие к узлам, которые уже включены в массив. Если узлы, принадлежащие этим элементам, еще не содержатся в массиве, они включаются туда. При решении контактной задачи контактным поверхностям тел условно приписываются понятия активной и пассивной. Активная поверхность принадлежит телу, на которое действуют внешние нагрузки (рис. 7.8). Если в массив порядка обхода узлов попадает один из контактных, то вместе с ним включается и сопряженный с ним, расположенный на контактной поверхности другого тела. Причем, на первое место всегда ставится узел, лежащий на активной поверхности.
Исследовано влияние порядка обхода узлов на задаче для прямоугольной пластины (рис. 7.9) [68]. При обходе узлов в порядке их нумерации решение с заданной точностью получено за 70 прогонок, при начале обхода от узла 9 с очередностью перебора узлов в порядке их удаления от этого узла — за 232 прогонки, при начале обхода от узла 19 — за 255 прогонок. Наибольшая скорость сходимости решения достигается, если обход начинается от тех узлов, для которых заданы в виде краевых условий смещения либо узловые силы.
Характер разделения области на конечные элементы также влияет на скорость сходимости решения. Скорость сходимости исследована на примере одноосного растяжения пластины [68]. На длине пластины в десять слоев расположены треугольные конечные элементы (рис. 7.10). Исследовались три варианта конечно-элементных сеток: равномерная, измельченная к заделке пластины и измельченная к месту приложения нагрузки. Для равномерной разбивки решение с заданной точностью получено за 670 прогонок, для разбивки, представленной на рис. 7.10, а — за 480 прогонок и для разбивки с измельчением элементов к месту приложения сил (рис. 7.10, б) — за 1400 прогонок. Наибольшая скорость сходимости решения обеспечивается, если к нагруженным узлам прилегают крупные конечные элементы.
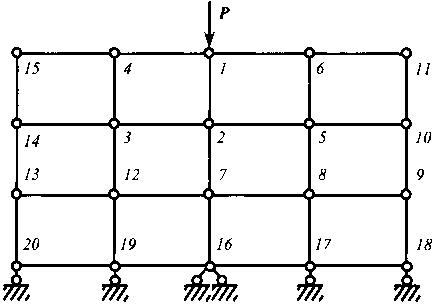
Рис. 7.9. Расчетная схема прямоугольной пластины

Рис. 7.10. Варианты конечно-элементной сетки пластины: а — со сгущением к заделке; б — со сгущением от заделки
