Для решения задач качения для тел с произвольными поверхностями катания и, в частности, для колеса и рельса с изношенными профилями применен алгоритм, описание которого приведено выше [172]. Рассматривалось качение при наличии продольного и поперечного крипов и спина. Отличительная особенность программ, реализующих алгоритм, состоит в наличии блока задания кинематики перемещения тел. В вычислительной процедуре использованы внешние итерации и внутренние итерации- прогонки. Во внешних итерациях, выполняемых с заданными шагами по времени, меняются краевые условия. Телам на каждом шаге задаются несогласованные по величине перемещения с тем, чтобы за счет их разности могли быть реализованы при моделировании качения крипы и спин. Во внутреннем цикле выполняются итерации-прогонки до получения достаточно малой величины невязки на каждом шаге по времени. Разработанный алгоритм решения контактной задачи качения отслеживает вход в контакт новых узлов и выход узлов из контакта на сбегающем крае, устанавливая при этом, контактируют ли узлы без проскальзывания или с проскальзыванием.
Алгоритм протестирован на задачах с известными аналитическими или численными решениями. В качестве тестовой задачи рассмотрено качение диска по границе полуплоскости с продольным крипом. Эволюция закона распределения касательных сил по длине контакта показана на рис. 10.22. Вначале диск прижат к полуплоскости, в результате чего образовался контакт длиной 12 мм. Качение началось без приложения касательной силы. Затем на каждом шаге по времени телам задавались перемещения: полуплоскости поступательное, а диску вращательное вокруг центра, несогласованность которых по величине позволила реализовать продольный крип различных значений. За 100 шагов по времени диск перекатился на расстояние 15 мм. На каждом шаге было получено распределение касательных нагрузок по длине контакта. Для некоторых шагов они представлены на рис. 10.22. На эпюрах, соответствующих 70 шагам при крипе 0,002 и 58 шагам при крипе 0,005, получены хорошо известные картеровские распределения, соответствующие установившемуся качению. Набегающий край контакта располагается справа, к нему прилегает участок сцепления. При меньшем крипе он имеет большие размеры. На участке скольжения, прилегающем к сбегающему краю, касательные силы ограничены силами трения скольжения.
Рассмотрены также хорошо изученные задачи качения трехмерных тел в условиях герцевского контакта с простым продольным крипом 0,002; чистым спином 0,00175 и задача качения с продольным крипом 0,002 и спином 0,0066. Взяты поверхности катания тел, близкие по форме к поверхностям катания колеса и рельса. Тело, моделирующее колесо, имело цилиндрическую или коническую (для получения спина) поверхность радиусом 50 см, а радиус поверхности катания тела, моделирующего рельс, принят 40 см. Для получения распределений касательных нагрузок по поверхности контакта, соответствующих установившемуся качению, понадобилось 80 итераций. Распределения касательных нагрузок, отношений касательных нагрузок к нормальным q/p и векторы касательных узловых сил при качении с реализацией заданных выше скольжений показаны на рис. 10.23.
При качении с продольным крипом I скольжение отсутствует на участке сцепления, прилегающем к набегающему краю, расположенному справа. Он имеет лимонообразную форму. Векторы касательных сил параллельны направлению качения. На эпюре отношений q/p хорошо виден участок скольжения. На этом участке отношение q/p равно коэффициенту трения скольжения. На эпюре он представлен горизонтальной площадкой. При качении с чистым спином II участок сцепления имеет форму клина с острием, расположенным на сбегающем крае. Он хорошо прослеживается как на эпюре q, так и на эпюре отношения q/p.
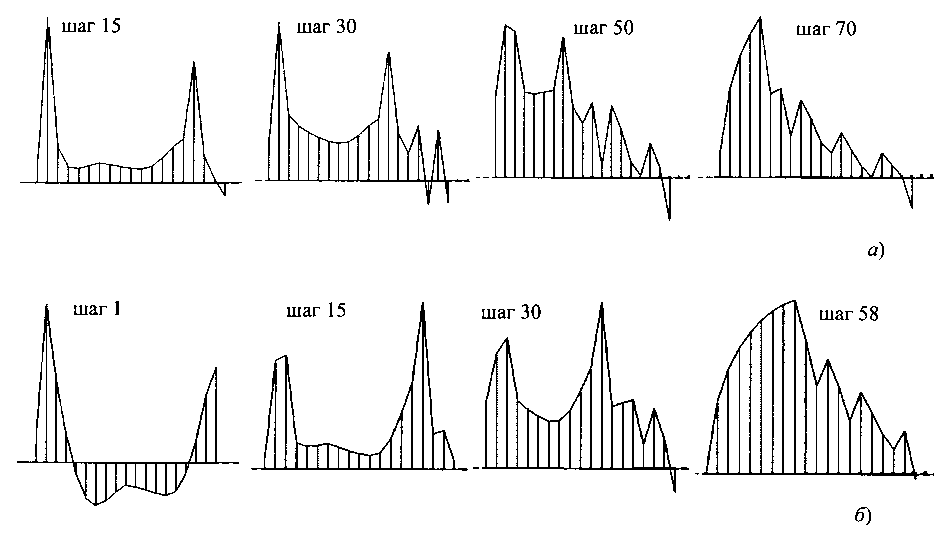
Рис. 10.22. Распределение касательных нагрузок по длине контакта при качении диска по полуплоскости с продольным крипом: а - х = 0,002; б - х = 0,005

Рис. 10.23. Распределение в контакте моделей колеса и рельса при качении: а - касательных нагрузок q; б- отношения касательных и нормальных нагрузок q/p; в - векторов касательных сил; I- слева направо с продольным крипом 0,002;
II- слева направо со спином 0,00175; III- справа налево с продольным крипом 0,002 и спином 0,0066
Направление касательных сил создает иллюзию потока, вращающегося вокруг некоторой точки, лежащей на сбегающем крае. Распределение касательных нагрузок при качении с продольным крипом и спином III полностью соответствует полученному в работах Д. Д. Калкера с помощью программы CONTACT.
При решении задачи качения колеса по рельсу в условиях конформного контакта взят профиль катания рельса с боковым износом 13 мм. Профили катания колеса и рельса на участках выкружек настолько близки, что в этой области возможен конформный контакт. Для конечноэлементных моделей колеса и рельса использована измельченная сетка из 72 300 конечных элементов и 51 000 узлов (рис. 10.24, а). На поверхностях контакта расположено 1288 пар узлов. Элементы, прилегающие к контактным поверхностям, имели размер 1 мм, как в поперечном направлении, так и в направлении качения. После введения моделей в контакт колесу было задано вертикальное перемещение 0,05 мм и горизонтальное 0,02 мм, что позволило получить в контакте вертикальную силу 93 кН и боковую 56,6 кН. Размер контактного пятна в направлении качения составил 10,2 мм. Распределение контактных давлений представлено на рис. 10.24, б. В продольном направлении оно описывается уравнением эллипса. По дуге профиля выкружки рельса давление меняется незначительно, но краевые эффекты проявляются. Кинематически было задано качение колеса с продольным крипом 0,001. За 51 итерацию колесо перекатилось на 9 мм. Распределения отношений q/p, соответствующих различному количеству шагов по времени перекатывания колеса, и векторы касательных сил показаны на рис. 10.25, а. Даже при столь малом продольном крипе почти по всему пятну контакта наблюдается скольжение. Направление векторов касательных сил скорее напоминает картину, полученную при качении со спином (рис. 10.25, б). Участок сцепления практически отсутствует.
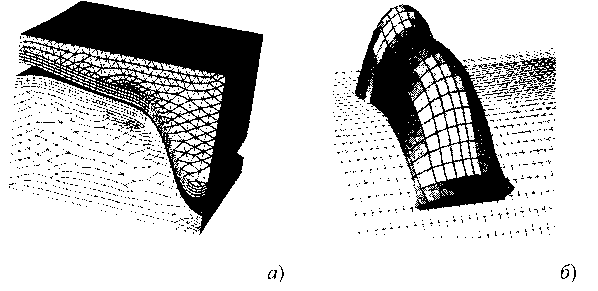
Рис. 10.24. Конечно-элементная модель колеса и рельса с конформными профилями выкружек (а) и распределение контактных давлений (б)
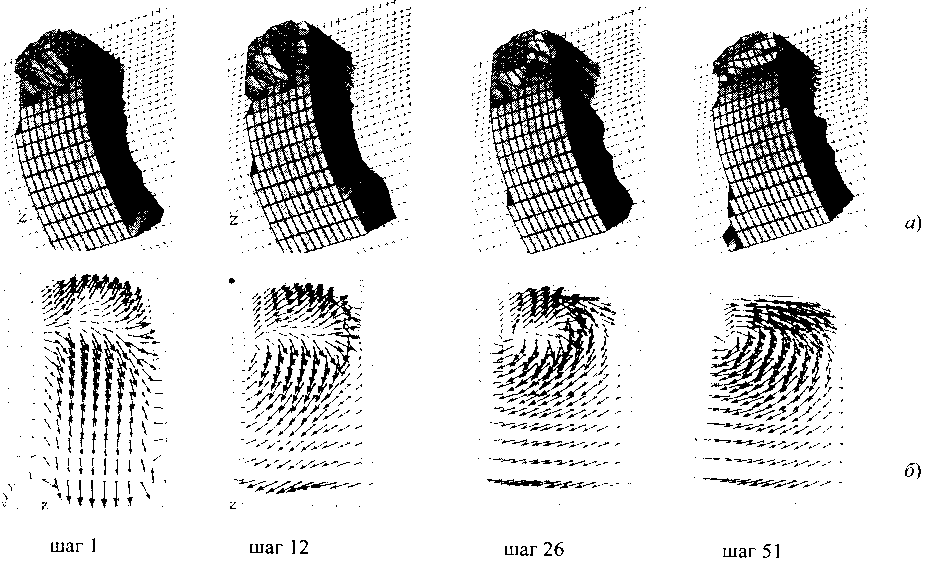
Рис. 10.25. Распределение q/р (а) и векторы касательных сил (б) при качении в условиях конформного контакта
