Определение сил методами математического моделирования. Один из эффективных способов определения сил взаимодействия колес подвижного состава с рельсами базируется на использовании математических моделей. Предложена комплексная математическая модель системы экипаж - тяговый привод - путь [42], охватывающая локомотивы с трехосными тележками, двухступенчатым рессорным подвешиванием, упругой связью колесных пар с рамой тележки и тележек с кузовом с учетом всех основных нелинейностей, присущих реальным локомотивам (рис. 10.4, рис. 10.5). При задании упругодиссипативных параметров приняты следующие допущения:
шкворни кузова упруго связаны в продольном направлении с рамами тележек связями достаточно большой жесткости сx*;
для описания диссипативных свойств резинометаллических опор кузова принята линейная модель вязкого трения с параметрами к*x ,кy*, к*z;
силы трения фрикционных гасителей буксового подвешивания и носиков тяговых двигателей по траверсе упругой подвески Fуп описываются кулоновой моделью.
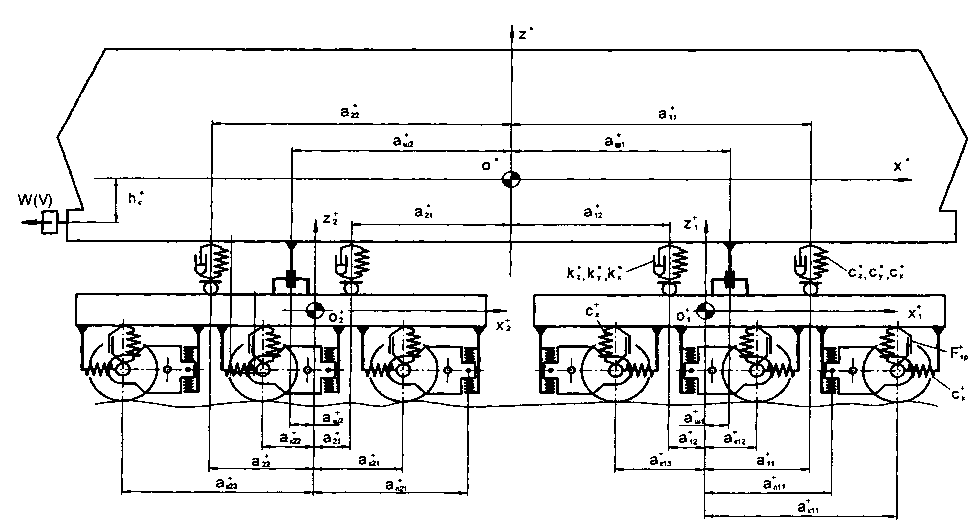
Рис. 10.4. Расчетная схема шестиосного локомотива
Рис. 10.5. Расчетные схемы:
а - локомотива с бесчелюстными тележками; б - колесно-моторного блока
Рис. 10.5. Продолжение
Математическая модель колесно-моторного блока с тяговым приводом учитывает упругую угловую связь колес через ось. Венец зубчатого колеса упруго через резинометаллические элементы с нелинейной силовой характеристикой связан с осью колесной пары. В зубчатом зацеплении учитывается зазор между зубьями 2δз, в подвеске двигателя к раме тележки упругая связь также нелинейная, она учитывает предварительный натяг пружин и зазор δп (рис. 10.5, б).
Модель пути в вертикальной плоскости принята дискретной с приведенными к колесу массой, жесткостью и демпфированием. В горизонтальной плоскости путь рассматривается как безынерционный упругий. Макрогеометрия пути учитывает наличие переходных кривых. Для описания переходной кривой в плане используется уравнение кубической параболы или радиоидальной спирали (10.2). Положение системы характеризуется 78-ю обобщенными координатами, в том числе шестью координатами кузова и каждой тележки и десятью координатами каждого из шести колесно-моторных блоков.
Для составления уравнений движения используются выражения для кинетической и потенциальной энергий системы. Для свободного твердого тела модели экипажа вводится тройная система координат: неподвижная инерциальная с помощью которой определяется абсолютная скорость объекта; подвижная система 0xyz, которая перемещается вместе с объектом поступательно и определяет линейные перемещения центра тяжести или любой другой его точки, принятой за полюс, и третья система координат, жестко связанная с телом, которая определяет угловые перемещения объекта вокруг центра тяжести или полюса. Таким образом, абсолютная скорость свободного твердого тела равна сумме скоростей поступательного движения его центра тяжести
и вращательных (сферических) движений вокруг полюса
При движении в кривой добавляется переносное движение с угловой скоростью ωο. В этих случаях уравнения движения можно записать разными способами и от выбора системы координат зависит сложность выражений для кинетической энергии системы. Наиболее удобным и простым является способ математического описания движения рельсового экипажа по криволинейному участку пути на основе теории относительного движения с использованием движущихся неинерциальных локальных систем координат с учетом сил инерции переносного движения. Ниже приведены дифференциальные уравнения движения для одного колесно-моторного блока.
Определены силы взаимодействия колесной пары и пути. К ним относятся силы крипа и нормальные реакции в точках контакта поверхности катания колес и рельсов, нормальная сила и сила трения, действующие в точке контакта гребня и боковой грани рельса при набегании (рис. 10.6). Используется модель двухточечного контакта набегающего колеса и рельса. В математической модели учитываются забег bх точки гребневого контакта А относительно вертикальной плоскости, проходящей через ось колесной пары, и положение точки А по высоте от поверхности катания колеса bz. Учет фактического положения точки контакта А гребня с рельсом при двухточечном контакте необходим при определении скорости и направления скольжения гребня по рельсу и оценке показателей износа.
Рис. 10.6. Схема действия сил в системе колесная пара - путь
В модели рельса (рис. 10.6, г) учтена возможность упругого отжатия его под действием поперечных сил: направляющей силы, силы крипа, проекции нормальной силы, действующей в точке 7, приложенных в виде реакций, и момента всех сил, действующих на рельс, и вызывающих его поворот.
Разработанная математическая модель пространственных колебаний тепловоза позволяет сравнивать и решать разнообразные задачи: исследовать динамические качества тепловоза; давать оценку изменения параметров экипажа в эксплуатации и при его модернизации; определять динамическую нагруженность привода, показатели износа колес; оценивать влияние силы тяги на динамику экипажа при движении на прямых и кривых участках пути, в том числе при различных триботехнических состояниях колес и рельсов, определяемых очертанием профилей и значением коэффициентов трения между колесом и рельсом; определять сопротивления движению, т.е. учитывать переменную скорость по угловой координате в кривой.
Для решения практических задач в Брянском государственном техническом университете разработан автоматизированный программный комплекс UM Loco [173]. Для учета особенностей моделирования рельсового экипажа разработаны алгоритмы определения положения точек контакта колес с рельсами с заданными профилями, расчета сил крипа и параметров путевой структуры, представленной неровностями рельсов и макрогеометрией колеи. В вычислительных процедурах используются эффективные численные методы Гира, Адамса, прогноз-коррекции, реализованы быстрые процедуры решения кинематически линеаризованных дифференциально-алгебраических уравнений движения. Разработаны процедуры генерирования случайных неровностей по заданным спектральным плотностям, а также периодических и единичных неровностей любого типа. Имеется возможность задания неровностей по данным натурных измерений. Создана визуальная среда для задания профилей колес и рельсов. Комплекс позволяет моделировать движение рельсового экипажа в режимах выбега и тяги в прямых и кривых участках пути. В комплексе реализована возможность выполнения многовариантных расчетов в соответствии с заданным планом численных экспериментов, при этом расчеты проводятся при различных значениях параметров, например, жесткости пружин, коэффициентов демпфирования, скорости и т.д.
Для формирования модели рельсового экипажа используется отдельный модуль комплекса UM Loco. Для каждого тела, включенного в модель, указывается масса и момент инерции, инерционные характеристики параметризуются.
Уравнения движения рельсового экипажа формируются на базе теоремы о движении центра масс и динамических уравнений Эйлера. В процессе синтеза уравнений движения производится их линеаризация по обобщенным координатам.
Для анализа динамики и оценки динамических качеств рельсовых экипажей в комплексе используются следующие переменные:
скорость движения;
ускорения в заданных точках кузова, рам, колесных пар, двигателей; относительные смещения и углы поворота тел;
углы набегания колесных пар на рельс;
значения активных сил и сил реакций: рамных, направляющих, боковых сил, сил, возникающих в тягах, гасителях, упругих элементах, усилий в зубчатых зацеплениях и т.д.;
силы крипа, продольный и поперечный крип, нормальные реакции в контакте колеса и рельса, трение на гребне при двухточечном контакте;
коэффициенты динамики;
факторы износа - работа трения, удельная работа и мощность сил трения на гребне.
Для переменных приняты следующие условные обозначения:
ГУ1 - горизонтальные ускорения передней части кузова;
ВУ1 - вертикальные ускорения передней части кузова;
- нормальная и касательная силы в точке контакта колеса с рельсом по кругу катания;
N2,F2 - нормальная и касательная силы в точке забега при двухточечном контакте;
Кд - коэффициент вертикальной динамики;
Yр - рамные силы;
Yб - силы отжатия рельса (боковые силы);
Yн - направляющие силы;
ПСТ - продольная сила трения в точке забега;
ПСКР - продольные силы в поводках;
ПРК - продольная сила крипа;
ППК - поперечная сила крипа;
Фс - фактор износа, определяемый по скорости скольжения;
Φκ - фактор износа, определяемый по времени контактирования гребня с боковой поверхностью рельса в прямой;
Фа - удельная работа сил трения;
ан - угол набегания колесной пары.
Разработанная методика предусматривает определение нескольких параметров, необходимых для расчета показателей износа. В качестве одного из критериев для оценки износа гребней колес в кривых используется фактор износа, предложенный С.М. Андриевским:
(10.19) где Yн - направляющая сила; а - угол набегания.
Учитывая, что в последние годы для уменьшения бокового износа широко применяется лубрикация гребней колес и рельсов, в формуле (10.19) учитывается коэффициент трения скольжения f в контакте гребня колеса с рельсом. Тогда она приобретает вид
(10.20)
При известной скорости скольжения в кривых vs целесообразно оценку производить по фактору, определяемому выражением
(10.21)
По физическому смыслу он представляет собой мощность трения.
При движении в прямых участках пути происходит периодическое набегание гребней колес на рельсы, и использование приведенных выше критериев износа теряет смысл. В этом случае удобно использовать критерий износа гребней колес как отношение времени tк контактирования гребня колеса и рельса к общему времени tм движения в прямой:
(10.22)
Разработаны алгоритмы задания профилей катания и определения положения точек геометрического контакта колеса и рельса. Качественным критерием достаточной гладкости профилей служит непрерывность численно рассчитанной производной от функций профилей.
Специальный алгоритм используется для определения минимального расстояния между профилями. Он позволяет для заданной точки на профиле рельса определить соответствующую точку на профиле колеса и расстояние между ними. Основными преимуществами алгоритма являются его надежность и независимость от гладкости задания профилей.
Разработана методика расчета сил, возникающих в контакте колеса и рельса. Введены переменные, определяющие деформации рельса в сечении, соответствующем положению каждого колеса.
Силы и момент, связанные с деформацией рельса, определяются соотношениями
(10.23)
Эти силы совместно с контактными силами, действующими на рельс со стороны колеса, должны быть самоуравновешивающимися. Силы, действующие в точках контакта на колесо в случае одноточечного и двухточечного контактов, приведены на рис. 10.8 (не показаны силы, действующие в продольном направлении).
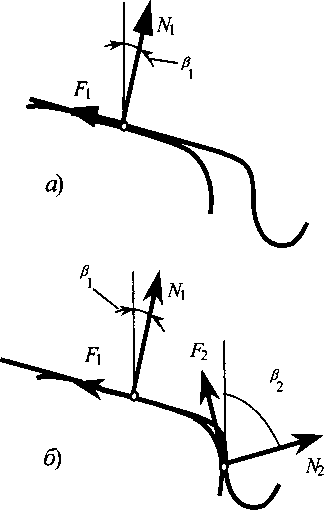
Рис. 10.8. Силы, действующие на колесо в точках контакта: а - одноточечного; б - двухточечного
Уравнения равновесия системы сил имеют вид в случае одноточечного контакта:
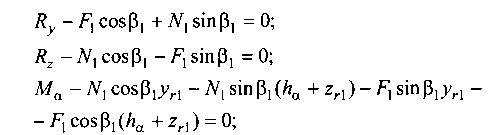(10.24)
для двухточечного контакта:
- Уравнения записаны в проекциях на оси системы координат пути.
Уравнения (10.23), (10.24) в случае одноточечного контакта и (10.23), (10.25) в случае двухточечного контакта представляют собой систему нелинейных уравнений относительно неизвестных деформаций рельса и нормальных сил реакций в точках контакта.
При исследовании динамики рельсового подвижного состава и решении задач взаимодействия колеса и рельса методами компьютерного моделирования необходимо находить точки контакта профилей бандажей и рельсов. Причем профили могут быть как новые, так и с различной степенью износа. В расчетном комплексе применены различные типы сглаживания профиля, которые используют Сплайн, Сплайн-2 или β-сплайн сегменты. Первые два соответствуют кусочно-кубическому сплайн- интерполированию соответственно по одной и двум координатам. Математический метод, известный как метод аппроксимации с помощью β-сплайнов, использован для получения гладких кривых удобным образом. Процедура, реализующая этот алгоритм, генерирует множество других точек путем интерполяции. Кроме того, есть возможность выделения сразу нескольких, а также всех сегментов стандартным способом.
В описанной методике компьютерного моделирования пространственных колебаний рельсовых экипажей изложены основные алгоритмы, которые легли в основу автоматизированного программного комплекса UM Loco. Комплекс позволяет автоматизировать интеллектуально трудоемкую процедуру формирования математических моделей пространственных колебаний рельсовых экипажей, а также быстро получить адекватную математическую модель, используя на стадии ее подготовки некоторые формализованные процедуры.