Установление закономерностей приближения значений перемещений узлов к их истинным значениям в процессе выполнения прогонок позволяет выработать обоснованные критерии окончания счета, а также прогнозировать его длительность по числу прогонок и времени. Исследование проведено на решении простейшей задачи для пластины, подверженной одноосному растяжению (рис. 7.3). Расчетная схема пластины представлена квадратными стержневыми конечными элементами. По ее длине располагается восемь слоев элементов. Число элементов в слое влияет на время счета. При увеличении числа элементов в слое от 5 до 40 время счета возрастает в 2 раза. К узлам слоя j=1 приложены внешние нагрузки, значения которых получены путем приведения распределенных нагрузок постоянной интенсивности, приложенных на торце пластины, к узлам конечно-элементной схемы. На нижние узлы слоя элементов j=8 наложены вертикальные связи. Истинные перемещения v узлов каждого слоя элементов находятся из элементарных зависимостей.
Закономерности приближения значений перемещений v к их истинным значениям для различных слоев расчетной схемы пластины в зависимости от числа прогонок п представлены на рис. 7.4. Значению 100 % на оси ординат соответствует истинное перемещение любого из восьми слоев узлов. Задача для рассматриваемой пластины решена с точностью 99 % по статическому критерию (7.8) за 121 прогонку.

Рис. 7.3. Конечно-элементная схема пластины, подверженной одноосному растяжению
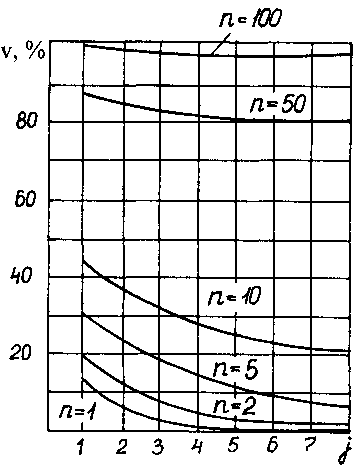
Рис. 7.4. Зависимости перемещений ν узлов слоев j от числа прогонок п для пластины с восемью слоями
На первых прогонках наибольшие перемещения получают узлы, в которых приложены внешние нагрузки. С увеличением числа прогонок неравномерность сглаживается. На 50-й прогонке все слои узлов выбирают 80 % значений их истинных перемещений. Скорость приближения перемещения узла к истинному значению на последних прогонках уменьшается. Так, прибавка перемещений узлов первого слоя на последующих 50 прогонках составляет всего 9 %.
С особой наглядностью это можно продемонстрировать на аналогичном примере для пластины с шестнадцатью слоями элементов по ее длине. Как и в предыдущем случае, она подвергается одноосному растяжению. Значения перемещений узлов, принадлежащих соответствующим слоям элементов, в процентном выражении по отношению к их истинным значениям представлены на рис. 7.5. Увеличение числа слоев элементов приводит к значительному росту числа прогонок, необходимых для достижения нужной точности. Для решения этой задачи с той же точностью, что и в первом случае, понадобилось 450 прогонок. На рис. 7.6 представлена зависимость перемещения узла третьего слоя этой пластины к истинному от числа прогонок п. Приращения перемещений на последних прогонках малы, и для достижения высокой точности необходимо выполнять все большее число прогонок.

Рис. 7.5. Зависимости перемещений ν узлов слоев j от числа прогонок п при числе слоев 16

Рис. 7.6. Зависимость перемещения ν узла слоя j=3 от числа прогонок
Необходимое для получения решения с заданной точностью число прогонок связано с числом слоев конечных элементов довольно сложным законом. Уточнять его нет смысла в связи с тем, что оно зависит, кроме того, от геометрической формы области и приложенных к ней нагрузок. Можно еще отметить, что быстрее всех устанавливается значение первой главной деформации и медленнее — второй.
Зависимость числа прогонок, необходимых для получения требуемой точности вычисления перемещений узлов, от числа слоев конечных элементов представлена на рис. 7.7. При числе слоев j=40 требуемое число прогонок nтр>3000.
На длительность счета влияет также порядок обхода узлов конечноэлементной схемы при выполнении итераций. Оптимальным является порядок обхода, при котором вначале выполняются итерации для узлов с заданными перемещениями, либо нагруженных внешними силами, затем ближайших к ним и остальных, расположенных в порядке их удаления.

Рис. 7.7. Зависимость требуемого числа прогонок wтр от числа слоев элементов j
Выполненные исследования позволяют рекомендовать в качестве методов ускорения сходимости итерационного процесса применение таких итерационных методов, как метод последовательной верхней релаксации, блочных итерационных методов, деформационного нагружения.
