Метод поузловых итераций для решения задач с нелинейностями и, в частности, контактных с использованием конечно-элементных расчетных схем предложен в работе [75] и получил развитие в работах [57, 68, 80, 83, 172]. Метод позволил решать как статические контактные задачи, так и задачи качения без введения каких-либо существенных ограничений на формы и размеры контактирующих тел, характер и последовательность приложения внешних нагрузок. Разработаны пакеты прикладных программ РСМКЭ, а затем RSFEM, позволяющие решать задачи с использованием плоских, осесимметричных и трехмерных расчетных схем, построенных на базе конечных элементов различного типа. Впоследствии блок решения контактных задач использован в расчетном комплексе DPMFеm [ 171 ].
Исследования влияния геометрических форм объектов, краевых условий и типа внешней нагрузки на скорость сходимости итерационных процедур выполнено на простейших стержневых конечно-элементных схемах, моделирующих сплошную среду. Стержневые конечные элементы не нашли применения для моделирования континуальных систем. Тем не менее, первые попытки решения задач строительной механики для тонкостенных балок с переменным по длине сечением, пластинчатостержневых систем, а также задач теории упругости методом конечных элементов связаны с применением стержневых элементов.
При решении плоской задачи теории упругости сплошная среда моделируется стержневой системой, в основе которой лежит прямоугольная ячейка, образованная шестью стержнями: четырьмя контурными и двумя диагональными [138, 134]. Стержни соединены между собой в узлах шарнирно и работают только на растяжение или сжатие. Аналогичный элемент использован в работе [51] с тем отличием, что контурные стержни ячейки жестко соединены между собой в узлах и обладают изгибной жесткостью.
При определении жесткостных характеристик стержней из условия эквивалентности податливостей элемента сплошной среды и стержневой ячейки возникают затруднения при произвольных значениях коэффициента Пуассона. Стержневой конечный элемент является наиболее простым элементом, компоненты матрицы жесткости для него легко могут быть получены. То обстоятельство, что он не нашел применения для моделирования сплошных сред объясняется еще и трудностью построения конечно-элементных сеток для областей сложных форм.
Тем не менее, рассмотрение метода поузловых итераций начнем, опираясь на элемент такого типа. Это связано с тем, что применение именно стержневого элемента привело к использованию в качестве вычислительной процедуры метода верхней релаксации, предложенного Р.В. Саусвеллом для стержневых систем [84]. Благодаря тому, что выполнению итерационной процедуры для узла расчетной схемы было поставлено в соответствие изменение физико-механического состояния расчетной схемы, был получен метод, позволяющий в единой итерационной процедуре учитывать ряд нелинейностей, в том числе, вносимую контактной задачей.
МЕТОД «РЕЛАКСАЦИИ»
При моделировании сплошной упругой среды стержневыми конечными элементами расчетная схема представляется в виде ферменной статически неопределимой стержневой системы. Возможности стержневого конечного элемента чрезвычайно ограничены. С его помощью можно смоделировать среду с коэффициентом Пуассона ν=1/3. Для получения зависимостей метода поузловых итераций использован наиболее простой стержневой конечный элемент — квадратный. Площади поперечных сечений стержней для квадратного конечного элемента [72]
![]() (7.1) где а - длина стороны элемента; t - толщина элемента; Аа, Ас - площадь поперечного сечения соответственно контурного и диагонального стержня.
(7.1) где а - длина стороны элемента; t - толщина элемента; Аа, Ас - площадь поперечного сечения соответственно контурного и диагонального стержня.
Раскрытие статической неопределимости расчетной схемы методом сил связано с трудностями при выборе основной системы и определении сил в стержнях, как от внешних нагрузок, так и от единичных неизвестных сил. Кроме того, удобно для конечно-элементной схемы получить решение в виде значений перемещений ее узлов. Такая информация позволяет наиболее просто определить деформации и напряжения в точках сплошной среды. Широкое применение для решения таких задач нашел метод перемещений, предполагающий наложение связей на все узлы расчетной схемы и выбор в качестве неизвестных перемещений узлов.
Система уравнений метода перемещений для определения неизвестных может быть представлена в виде
KU = R, (7.2)
где К — матрица жесткости; U — вектор узловых перемещений; R — вектор узловых сил.
Компоненты матрицы жесткости представляют собой силы, возникающие в наложенных на узлы связях, при единичных смещениях узлов.
Для решения системы уравнений (7.2) чаще всего используются прямые методы: метод Гаусса, LDL-факторизация, разложение Холецкого, фронтальный и др. Из итерационных нашли применение методы Гаусса-Зейделя, метод последовательной верхней релаксации, градиентные методы групповой и блочной итерации. При применении итерационных методов на каждом шаге получается очередное приближение вектора перемещений узлов. На последующем шаге значения перемещений уточняются. Для расчета плоского напряженного состояния пластин использован метод Зейделя [2]. Отмечена малая скорость сходимости этого процесса, особенно на завершающем этапе решения. Тем не менее, итерационные методы могут обеспечить и некоторые преимущества при решении задач.
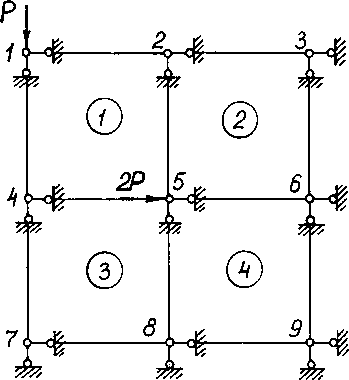
Рис. 7.1. Расчетная схема прямоугольной пластины с четырьмя стержневыми элементами
Рассмотрим прямоугольную пластину, закрепленную по нижней кромке, которая нагружена силами Р и 2Р (рис. 7.1). Она представлена четырьмя прямоугольными стержневыми элементами. Система уравнений, в виде удобном для применения метода итераций, содержит шесть векторных уравнений:
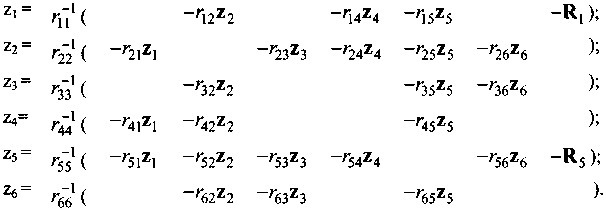
Каждое уравнение содержит два скалярных, в которых приравниваются нулю реакции, возникающие в каждой из связей, наложенных на узел.
При решении системы уравнений (7.3) нет необходимости записывать ее в явном виде и строить матрицу жесткости всей системы. Для решения одного уравнения системы на очередной п-й итерации необходимы векторы перемещений узлов, соединенных стержнями с рассматриваемым, полученные частично на (п-1)-й, а частично на п-й итерации, и компоненты матрицы жесткости, соответствующие перемещениям соседних узлов. Последние могут храниться в виде плотно упакованного массива, либо вычисляться на очередной итерации при использовании простых конечных элементов. Таким образом, при применении итерационного метода отпадает необходимость в хранении матрицы жесткости, либо ее блоков в оперативной памяти машины. Вместе с тем отпадают проблемы оптимизации нумерации узлов конечно-элементной схемы для получения минимальной ширины ленты матрицы жесткости.
Если не абстрагироваться при решении уравнений (7.3) от расчетной схемы и в соответствии процедуре вычисления вектора перемещений поставить изменение состояния расчетной схемы, то можно найти еще ряд преимуществ, связанных с применением итерационного метода. Два скалярных уравнения, соответствующие первому векторному уравнению, предназначены для определения перемещений узла 1 по осям х и у. При решении первого уравнения используются величины перемещений узлов 2, 4 и 5, найденные на предыдущей итерации постоянные при выполнении итерации для узла 7, т.е. выполнению такой итерации соответствует перемещение узла 1 по оси х в равновесное состояние при освобождении его от горизонтальной связи, и закрепленных в смещенных положениях соседних узлах расчетной схемы.
Решению второго уравнения соответствует освобождение узла 1 от связи по оси у и перемещение его по этому направлению в равновесное положение. При освобождении узла 1 сразу от двух связей он получает перемещение по двум осям. Для их определения необходимо решить совместно два первых скалярных уравнения. Такой итерационный метод носит название блочного. В блок могут объединяться перемещения нескольких узлов. При объединении в блок перемещений узла 1 на очередной итерации он получает прибавку перемещений за счет деформирования лишь одного элемента 7. На рис. 7.1 номера элементов обведены кружками. При объединении в блок перемещений узлов 1, 2 и 4 совместно решаются шесть скалярных уравнений, соответствующих первому, второму и четвертому векторным уравнениям системы (7.3). Такому решению соответствует освобождение этих узлов от связей и, очевидно, при такой итерации узел 7 получит большие прибавки перемещений за счет деформации элементов 1, 2 и 3.
Аналогичная трактовка итерационной процедуры дана Р. В. Саусвеллом для расчета сложных ферменных конструкций [84]. Предложенный им метод назван методом «последовательной релаксации связей» (The Method of Systematic Relaxation of Constrains). Таким образом, недостаток метода — малая скорость сходимости в какой-то мере может быть устранен применением блочной процедуры, а также других итерационных методов решения.
Необходимо отметить еще одно важное преимущество итерационного метода. Он позволяет в единой итерационной процедуре учесть геометрическую и физическую нелинейности, а также открывает хорошие перспективы решения контактных задач благодаря тому, что появляется возможность следить за перемещениями узлов при выполнении итераций, устанавливать момент вхождения в контакт узлов, лежащих на контактных поверхностях, и с учетом трения в контакте определять величины компонентов контактных сил.
Итерационные зависимости для определения перемещений узлов расчетной схемы.
Для решения задачи итерационным методом необходимы зависимости, позволяющие найти уточненное значение перемещений i-го узла расчетной схемы на очередной итерации. При блочной итерации с объединением в блок перемещений ui и νi узла i задача сводится к определению его перемещений в равновесное положение при освобождении его от связей и закрепленных в смещенных положениях окружающих узлах. Схема элементов, прилегающих к узлу i, с обозначением узлов, размеров ячеек и жесткостей стержней представлена на рис. 7.2. Жесткость контурных стержней обозначена ЕА. Для стержней на стыке двух элементов жесткость удваивается. На узел i действуют внешние силы Fxi и Fyi. Перемещения соседних узлов считаются известными. Канонические уравнения метода итераций имеют вид
![]() (7.4) где rij - компоненты матрицы жесткости, по физическому смыслу представляющие собой силы, возникающие в i-й связи узла i при смещении его в направлении j-й связи на единицу; RiF - силы, возникающие вi-й связи от узловых сил Fi и смещений соседних узлов.
(7.4) где rij - компоненты матрицы жесткости, по физическому смыслу представляющие собой силы, возникающие в i-й связи узла i при смещении его в направлении j-й связи на единицу; RiF - силы, возникающие вi-й связи от узловых сил Fi и смещений соседних узлов.
Реакции, помноженные на а/ЕА, возникающие в связях 1 и 2 при смещении соседних узлов, представлены в табл. 7.1.
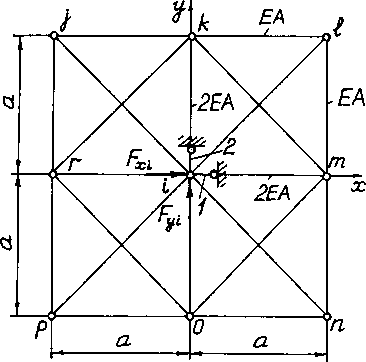
Рис. 7.2. Схема сил, действующих на внутренний узел расчетной схемы
7.1. Реакции, домноженные на а/ЕА, возникающие в связях, наложенных на узел Ζ, при смещении соседних узлов

Подстановка значений коэффициентов матрицы жесткости в систему уравнений (7.4) позволяет получить два уравнения для уточнения перемещений узла i на очередной итерации:
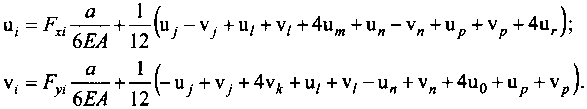
(7.5).
При использовании сетки из квадратных стержневых элементов удобно не приписывать номера ее узлам, а отождествлять номер узла с относительными координатами i и j. Приписывая перемещениям узлов индексы, совпадающие с относительными координатами узла, зависимости (7.5) можно представить в более удобном для алгоритмизации виде:
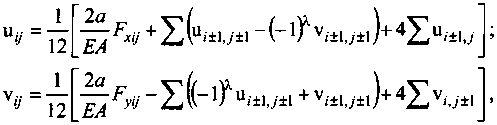
(7.6)
где λ=1, если знаки единиц, прибавляемых к i и j в нижних индексах, совпадают и λ=2, — если не совпадают.
Зависимости (7.6) могут быть использованы также для узлов, лежащих на контуре области. В этих случаях в них опускаются слагаемые, соответствующие индексы которых меньше imin или jmin, либо больше imax или jmax. При этом для узлов, лежащих на контуре и имеющих одну из координат ту же, что и узел ij, вместо множителя 4 необходимо ввести множитель 2. Уменьшение множителя в 2 раза объясняется тем, что эти узлы связаны с узлом ij одним контурным стержнем, а не двумя, как это имеет место для внутреннего узла. Поэтому при смещении узла, вызывающем растяжение такого стержня, в нем возникает сила, а значит и реакция в связи узла i, j, в 2 раза меньшая, чем для внутреннего узла. Кроме того, для таких узлов в зависимостях (7.6) необходимо в 2 раза увеличить общий множитель, стоящий перед скобками.
Не будем останавливаться на вычислении деформаций и напряжений в точках расчетной схемы. После определения перемещений ее узлов они находятся с использованием известных зависимостей для конечных элементов, моделирующих континуальную среду.
Критерии окончания счета.
Итерации для всех узлов сетки выполняются в некоторой последовательности, которая может быть неизменной при повторениях процедуры, а может и меняться. Назовем процедуру последовательного выполнения итераций для всех узлов сетки прогонкой. Решение задачи достигается путем многократного повторения прогонок. На итерациях первых прогонок уточнение перемещений идет за счет больших прибавок, при приближении к точному значению перемещения узла прибавки становятся все меньше.
При решении задач теории упругости может выбираться критерий, связанный с физическим смыслом задачи. В качестве таких критериев могут использоваться уравнения равновесия сил, действующих на всю расчетную схему, либо на ее отсеченную часть,
![]() (7.8) где Fi — внешняя узловая сила; Fi0 — внешняя узловая сила, приложенная к отсеченной части расчетной схемы; R — реакция в наложенной на расчетную схему связи; S — равнодействующая внутренних сил, возникающих по линии разреза.
(7.8) где Fi — внешняя узловая сила; Fi0 — внешняя узловая сила, приложенная к отсеченной части расчетной схемы; R — реакция в наложенной на расчетную схему связи; S — равнодействующая внутренних сил, возникающих по линии разреза.
Одним из наиболее удобных и универсальных критериев является норма вектора невязок. Итерационное уравнение (7.5) можно преобразовать к виду
![]() ).
).
Это равенство выполняется, если в него подставить значения перемещений, найденных при выполнении итерации для узла i. Затем могут быть выполнены итерации для части узлов, перемещения которых входят в это уравнение. При подстановке в него новых значений перемещений равенство не будет выполняться. Значение левой части представляет собой невязку. Невязка равна реакции Rxi в связи, наложенной на узел i. качестве критерия окончания счета удобно взять норму вектора невязок
![]() (7.9) где k - число узлов конечно-элементной схемы.
(7.9) где k - число узлов конечно-элементной схемы.
В случае если все узлы используются при вычислении критерия, признаком окончания счета является монотонное приближение нормы вектора невязок к значению квадратного корня из суммы квадратов реакций в необходимых для обеспечения статического равновесия связях расчетной схемы. Если эти узлы исключаются при вычислении критерия, то норма вектора невязок должна стремиться к нулю. При выполнении достаточно точных расчетов можно рекомендовать завершать счет, когда норма вектора невязок становится меньше
![]()
(где Fi — — внешняя узловая сила). При краевых условиях другого рода (заданных перемещениях узлов, соединениях деталей с натягом, температурных задачах) задать значение критерия в таком виде не удается. Исследования особенностей итерационной процедуры показали, что в этих случаях норма вектора невязок достигает наибольшего значения примерно на десятой прогонке.
В этих случаях счет завершается, когда критерий становится меньше величины
![]() — значение критерия на 10-й прогонке).
— значение критерия на 10-й прогонке).
