§ 14.8. ОСОБЕННОСТИ КОНСТРУИРОВАНИЯ И РАСЧЕТА РЕДУКТОРОВ МОТОР-КОЛЕС
Установка в планетарной передаче нескольких сателлитов, необходимость их равномерного размещении и равномерного распределения нагрузки между ними, соосное расположение основных звеньев, ограничение геометрических соотношений между элементами редуктора (шестернями, подшипниками и т. п.) выдвигают при проектировании планетарных редукторов ряд условий, которые для простых передач были необязательными или имели второстепенное значение.
Условие соосности относится только к планетарным передачам с цилиндрическими колесами. Оно предусматривает совпадение геометрических осей центральных колес, которое выполняется при соблюдении определенного соотношения числа зубьев или геометрических размеров, для планетарной передачи, показанной на рис. 14.16, а, это условие будет следующим:
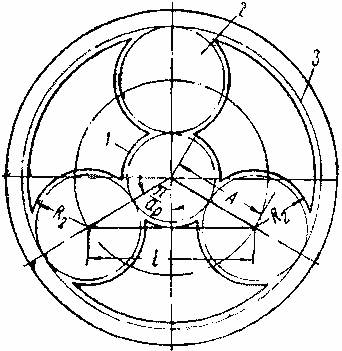
Рис. 14.19. Схема расчета условия соседства планетарной передачи
1 — солнечная шестерня; 2 — сателлит; 3 — коронная шестерня
Отношение усилия, воспринимаемого наиболее загруженным сателлитом, к усилию, воспринимаемому сателлитом, найденным в предположении равномерного распределения нагрузки, называют коэффициентом неравномерности Ω. Неравномерность распределения нагрузки между сателлитами приводит к увеличению габаритов передачи.
Один из способов выравнивания нагрузки между сателлитами состоит в применении «плавающих» основных звеньев, конструкция которых предусматривает возможность их самоустановки.
Перемещение «плавающего» звена при этом может обеспечиваться как за счет зубчатых соединений муфт основных звеньев, так и за счет упругих свойств деталей основного звена. Например, в конструкции мотор-колеса (см. рис. 13.16), редуктор которого выполнен по схеме 6 табл. 14.1, плавающими звеньями в каждом планетарном ряду являются солнечные шестерни, самоустанавливающиеся за счет упругих свойств торсионных валов, на концах которых они закреплены.
При неточном изготовлении и деформации элементов передачи нагрузка по длине зуба в планетарных передачах распределяется неравномерно. Это обстоятельство ограничивает ширину зубчатого колеса b, которая обычно принимается из условия b≤0,7d1, где d1 — диаметр меньшего зубчатого колеса.
Для того чтобы получить минимальные габариты и уменьшить скорость вращения сателлитов первой (быстроходной) ступени, ее передаточное отношение назначают возможно большим. С этой же целью следует назначать для наименьшей шестерни минимально допустимое число зубьев. Из условия отсутствия подрезания зубьев его принимают равным: 14-17.
Для повышения несущей способности н снижения габаритов планетарных передач применяют коррегированное зацепление, значительно увеличивающее долговечность, изгибную и контактную прочность передачи.
Динамические нагрузки могут снижаться также при фланкировании зубьев, т. е. при искусственном искажении профиля вершины зубьев путем специальной обработки (шлифовки по копиру).
Технологичность конструкции редуктора мотор-колеса может быть улучшена при унификации зубчатых колес и их модулей. Равнопрочность зацеплений в этом случае достигается изменением ширины колес.
Одной из трудностей при проектировании является подбор подшипников качения сателлитов. В этом случае необходимо выбирать толщину обода сателлита не менее 2,25 m, а максимально допустимый диаметр его наружного кольца не более m(z2—z1) мм. Минимальных габаритов сателлита и необходимой прочности его оси достигают применением игольчатых подшипников вместо шариковых и роликовых. Для этой же цели опоры качения могут выполняться без специальных колец. Дорожками качения роликов в этом случае служат сами оси сателлитов, а в качестве наружного кольца используется его обод. Опорные подшипники сателлитов рассчитывают на нагрузку Рс и скорость вращения w20 относительно водила, которые определяют по формулам:
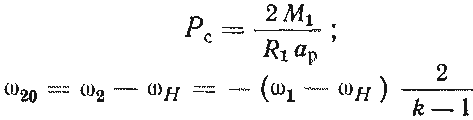(14.45)
(14.46)
Диаметральные габариты редукторов мотор-колес предварительно определяют из условий обеспечения примерного равенства диаметральных габаритов планетарных рядов и условий их равнопрочности. Пользуясь характеристиками, применяемыми при расчетах на прочность, можно получить семейство зависимостей диаметра делительной окружности коронной шестерни от передаточного числа і и момента нагрузки на ступице колеса Мс для схем редукторов мотор-колес, составленных из двух планетарных рядов.
Для редуктора, составленного из двух планетарных рядов с числом сателлитов ар=3 в каждом ряде, такая зависимость показана на схеме а (рис. 14.20). На схеме б показано относительное изменение диаметральных габаритов передачи, выполненной по схеме 8 (см табл. 14.1), и обычного планетарного ряда.
