Характерными особенностями редукторов тяговых передач при осевой подвеске двигателя и индивидуальном приводе колес являются:
- жесткое соединение несущих неподвижных деталей редуктора с корпусом тягового двигателя;
- жесткие габаритные ограничения размеров редуктора внутри обода колеса как в осевом, так и в радиальном направлениях;
- отсутствие специального корпуса редуктора, роль которого выполняет в большинстве случаев ступица колеса.
Редукторы мотор-колес по типу примененных кинематических схем могут быть планетарными, непланетарными и комбинированными (т. е. состоящими из планетарных и непланетарных механизмов), а по расположению осей входного и выходного валов — соосными и несоосными.

Рис. 14.16. Трехзвенный планетарный механизм (а) и его варианты при различном затормаживании его основных звеньев (б, в, г)
Большинство редукторов мотор-колес имеют одну-две ступени, с внутренним зацеплением, которое обладает большей несущей способностью по сравнению с внешним зацеплением и более полно отвечает условиям компоновки агрегатов мотор-колеса, позволяя уменьшить диаметральные размеры передачи.
Подавляющее большинство конструкций редукторов мотор-колес явЛЯЮТСЯ соосными по отношению к оси электродвигателя и колеса. Такое расположение элементов передачи позволяет использовать в ряде случаев корпус двигателя в качестве оси колеса, что значительно уменьшает вес узла.
Наиболее целесообразным типом зубчатой передачи (в том числе и соосной) сочетающей внешнее и внутреннее зацепление, является планетарная передача (планетарный механизм). При ее использовании значительно снижаются нагрузки на зубья, диаметральные размеры передачи и ее вес. Кроме того, рациональные типы планетарных передач позволяют снизить потери на трение, повысить надежность передачи, улучшить ее виброакустические свойства, а также обеспечить высокое значение передаточного числа при сравнительно небольших габаритах передачи.
Планетарным называется зубчатый механизм, в котором имеется одно или более зубчатых колес с подвижной осью. Этим он отличается от простых зубчатых механизмов, не имеющих подвижных осей зубчатых колес. На рис. 14.16, а изображен простейший планетарный механизм с одним внешним и одним внутренним зацеплением. Механизм этого типа наиболее часто используется в конструкциях редукторов мотор-колес. Звено, на котором устанавливаются зубчатые колеса с подвижными осями, называется водилом и обозначается буквой Н. Зубчатые колеса 2 с подвижными осями называются сателлитами. Неподвижная ось вращения механизма называется основной осью. Зубчатые колеса 1 и 3, сцепляющиеся с сателлитами, называются центральными колесами. Их ось вращения совпадает с основной осью.
Иногда внутреннее зубчатое колесо 1 называют солнечной шестерней, а внешнее 3 — коронной или эпициклической шестерней. Звенья, вращающиеся около основной оси и воспринимающие нагрузки от внешних моментов, называются основными звеньями. Механизм, изображенный на рис. 14.16, а, часто называют трехзвенным планетарным механизмом типа 2К-Н с внешним и внутренним зацеплениями. Индекс 2К-Н означает, что механизм из трех основных звеньев имеет два центральных зубчатых колеса и одно водило. Такую планетарную передачу иногда для краткости называют также планетарным рядом. Существуют планетарные зубчатые механизмы и других типов.
Для того чтобы планетарный механизм передавал крутящий момент, необходимо зафиксировать одно из его основных звеньев. Затормаживая, например, неподвижное колесо 3, получим передачу, в которой ведущим и ведомыми звеньями являются звенья 1 и Н или Н и 1 (схема б). Закрепив звено 1 (схема в), получим передачу с ведущим и ведомым звеньями 3 и Н или Н и 3. Если закрепить водило Н (схема а), то из планетарного механизма получится простой (т. е. непланетарный) с ведущим и ведомыми звеньями 1 и 3 или 3 и 1.
Планетарные механизмы, в которых подвижны все три основных звена, называются дифференциальными.
Передаточным отношением (или передаточным числом) і планетарного механизма называют отношение угловой скорости ведущего вращающегося звена к угловой скорости ведомого вращающегося

Верхний индекс при і соответствует заторможенному основному звену. Первый индекс снизу соответствует основному ведущему звену, второй — основному ведомому звену.
Передаточные отношения планетарного механизма легко определить из плана скоростей, пользуясь его геометрическими соотношениями.
На рис. 14.17, а показан план линейных скоростей трехзвенного планетарного механизма, выполненного по схеме б (см. рис. 14.16).
Здесь величины v1 и v3 — окружные скорости точек, расположенных на начальных окружностях зубчатых колес, vН — окружная скорость оси вращения сателлита:
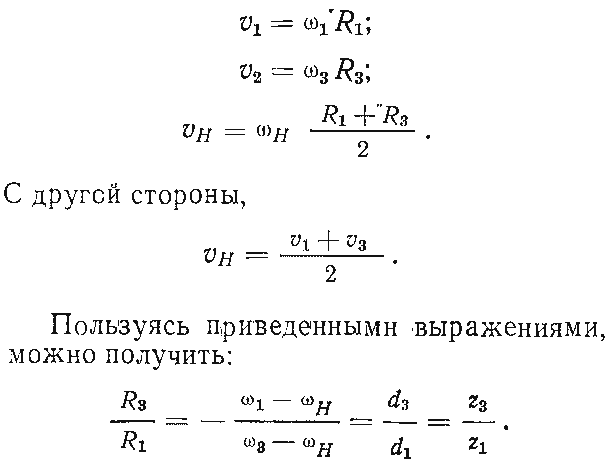

Рис. 14.17. План линейных скоростей (а) и схема нагрузок (б) трехзвенного планетарного механизма

В редукторах мотор-колес применяют исключительно механизмы, понижающие скорость вращения тягового электродвигателя. Поэтому из вариантов, показанных на рис. 14.16, обычно используются варианты б и г, у которых ведущим звеном является звено 1, а ведомым — звено 11 или 3. Таким образом, применение одного планетарного ряда в редукторе мотор-колеса может обеспечить снижение скорости вращения в k или k+1 раз (в зависимости от выбора ведомого звена). Величина k обычно выбирается в пределах 2—5. Следовательно, максимальное передаточное число, обеспечиваемое одним планетарным рядом, равно 6.
Полученные выражения (14.33) позволяют также определить направление вращения ведомого звена: на него указывает знак, стоящий перед абсолютным значением передаточного отношения.
Рассматривая различные схемы редукторов мотор-колес, сконструированных на базе трехзвенных планетарных механизмов типа 2К-Н с внешним и внутренним зацеплением, можно получить соответствующие формулы для определения передаточных отношений редуктора мотор- колеса в целом. Эти формулы и возможные пределы изменения абсолютных значений передаточного отношения для каждой схемы приведены в табл. 14.1.
Таблица 14.1
Расчетные зависимости для определения передаточных отношений планетарных редукторов мотор-колес
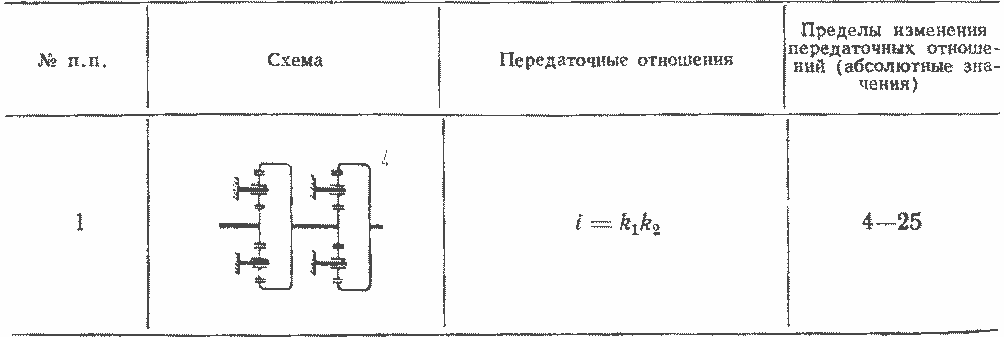
Продолжение табл. 14.1
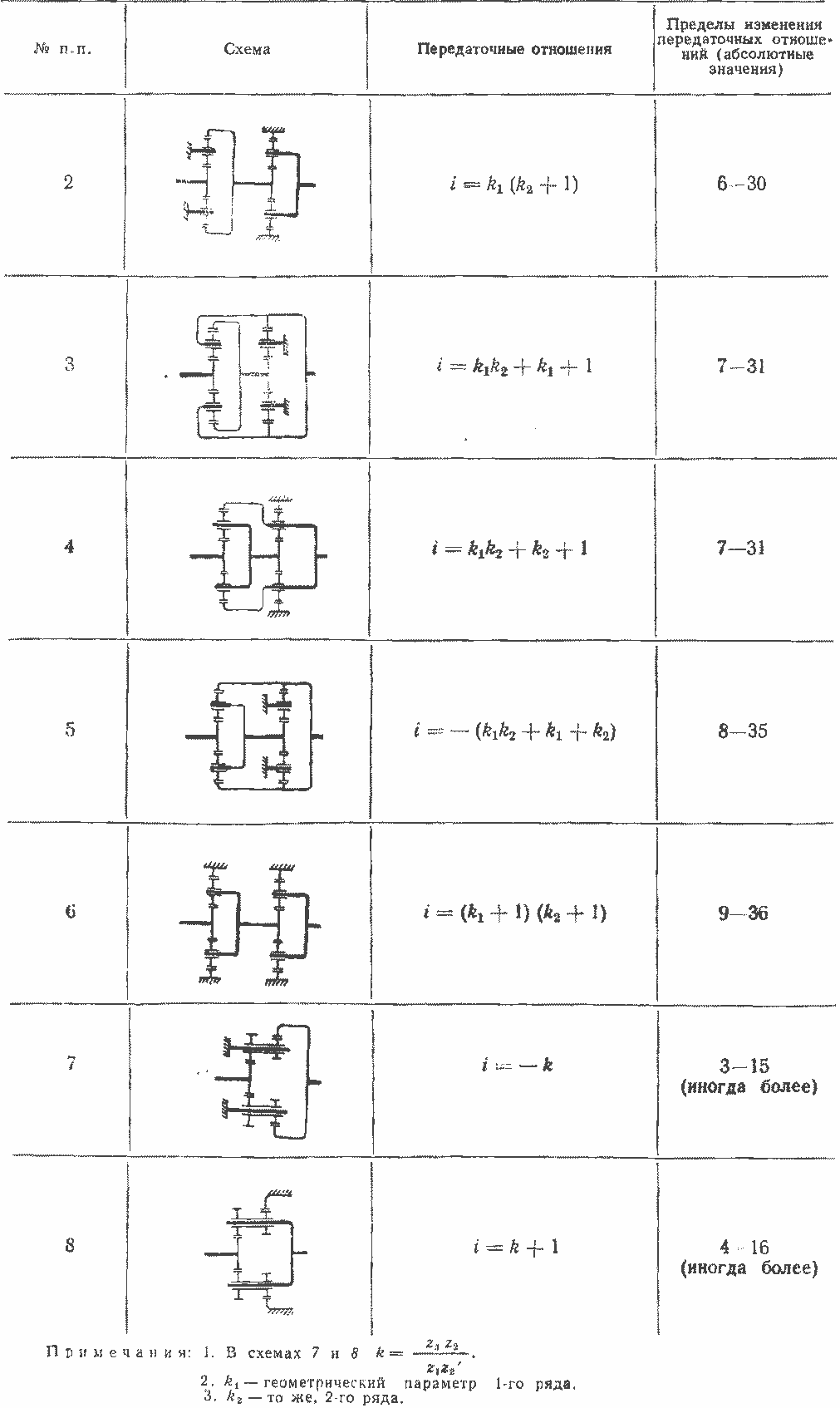
Схема 1 представляет собой два последовательно соединенных трехзвенных механизма с заторможенным водилом (т. е. два простых механизма). Схема 2 составлена из одного планетарного ряда, последовательно соединенного с простым механизмом, состоящим из зубчатых колес с внешним и внутренним зацеплением.
Схемы 5, 4 и 5 представляют собой составной двухрядный планетарный механизм. В этих схемах два каких-либо основных звена одного планетарного ряда жестко соединены с двумя основными звеньями второго планетарного ряда. Мощность в этих механизмах разделяется на два потока, соединяясь на выходном звене.
Схема б состоит из двух последовательно соединенных планетарных рядов. Схемы 7 и 8 используют только один планетарный ряд, но со сдвоенными сателлитами, позволяющими увеличить передаточное отношение механизма.
Конструктивно сдвоенный сателлит выполняется как две шестерни, жестко соединенные между собой н имеющие общую ось вращения. Шестерня большего диаметра имеет зацепление с солнечной шестерней, шестерня меньшего диаметра — с коронной.
В схеме 7 водило заторможено, следовательно, в данном случае также использован простой механизм.
Для расчета шестерен, подшипников, других деталей и узлов редуктора мотор-колеса необходимо определить силы и моменты, действующие на звенья планетарной передачи.
Если у планетарного механизма 2К-Н (см. рис. 14.16, а) известна величина момента М1, приложенного к солнечному колесу, то, пользуясь известными геометрическими соотношениями, можно определить и величины моментов, приложенных к другим звеньям механизма.
Для упрощения вывода зависимостей предположим (см. рис. 14.17, б), что имеется только один сателлит, и опустим радиальные составляющие нормальных усилий в зацеплениях, поскольку моменты от них относительно основной оси равны нулю.
Полагая, что момент направлен по часовой стрелке, найдем, что окружное усилие Р1, приложенное к зубьям колеса 1, равно:
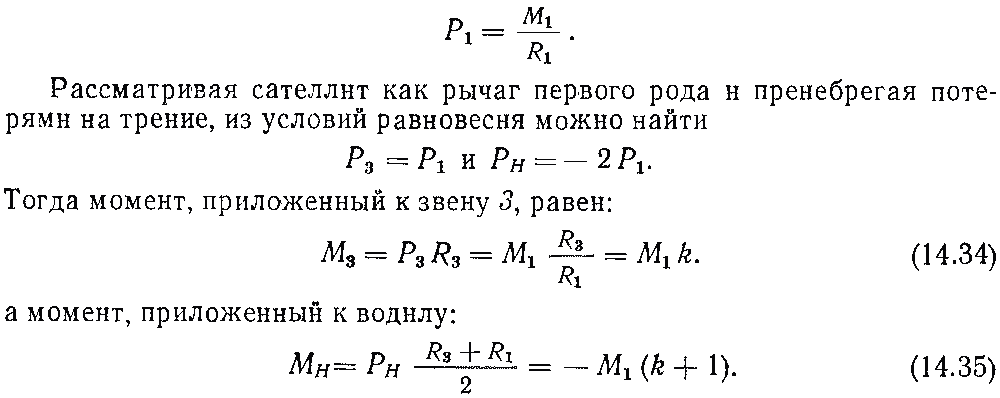
В результате вращения деталей передачи возникают потери в зацеплениях шестерен, в подшипниках, уплотнениях, а также потери, обусловленные разбрызгиванием и перемешиванием смазки в редукторе.
К. п. д. передачи может быть определен общим выражением
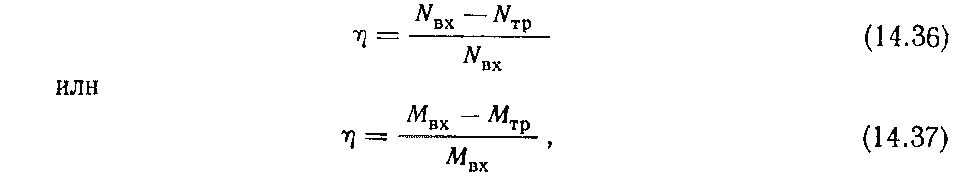

Приведенные формулы могут быть применены для определения к. п. д. зацеплений планетарного ряда со сдвоенными сателлитами.

Этой формулой учитывается также и потери, зависящие от скорости вращения, температуры и прочих параметров, так как экспериментально показано, что момент холостого хода планетарного редуктора в основном определяется потерями на трение при перемешивании и разбрызгивании масла, т. е. его уровнем, температурой, сортом, скоростью вращения и т. п.
