Глава 2. ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОГО ПОВЕДЕНИЯ СИСТЕМЫ «ПУТЬ—ПОДВИЖНОЙ СОСТАВ»
Расчетная схема системы «экипаж—путь»
Структура математической модели формируется в соответствии с теми задачами, которые ставятся при исследовании. При этом вводятся допущения, которые позволяют максимально упростить модель без потери интересующей информации об исследуемом объекте и протекающих в нем процессах [64—66].
В данном случае экипаж электровоза ВЛ80 (как наиболее распространенный на дорогах России) представлен в виде дискретной трехмассовой системы с постоянными и линейными инерционными и упруго-диссипативными связями, параметры которых приведены к одному колесу.
При составлении модели принимаются следующие допущения:
—рассматриваются только вертикальные колебания системы в продольной плоскости;
—неравномерность нагружения различных колес экипажа, обусловленная колебаниями галопирования кузова и тележек, а также боковой качкой, не учитывается, так как не является определяющей в формировании максимальных динамических нагрузок при взаимодействии колеса с рельсом;
—движение экипажа рассматривается в прямолинейных участках пути, так как именно в прямолинейных участках пути локомотив реализует весь свой скоростной режим в диапазоне 20—120 км/ч;
— кузов, рамы тележек и колесные пары считаем абсолютно жесткими телами;
—средние диаметры колес одинаковы;
—путь равноупругий;
—локомотив движется по рельсовому пути с вертикальными неровностями, одинаковыми для обеих рельсовых нитей.
На каждую тележку приходится половина массы кузова; вертикальные жесткость и коэффициент сопротивления центрального подвешивания на тележку соответственно равны 2СТ и 2βТ; масса надрессорных и неподрессоренных частей тележки соответственно равны тmи тн. Для одного колеса эти величины будут в 4 раза меньше, т. е. 1/8 т, 1/4 тт, 1/2 С и 1/2 β; Ст и βт.
Примем следующие обозначения:
т — масса кузова локомотива;
тт—масса обрессоренных частей тележки локомотива;
тн—масса необрессоренных частей локомотива (колесная пара);
тр—приведенная масса рельса Р65;
тш —масса шпалы;
тб —приведенная масса балласта;
О, От, Он, Ор, Ош, Об — соответствующие центры масс.
Модель пути представлена в виде трехмассовой системы с сосредоточенными параметрами и учитывающими колебания рельса, шпалы и балласта. Инерционные и упруго-диссипативные характеристики модели пути приведены к одному колесу.
Таким образом, имеем линейную шестимассовую динамическую систему, кинематически возмущаемую неровностями пути в контакте колеса с рельсом. Расчетная схема системы показана на рис. 2.1.
Методика исследования динамической системы
Как показывают многочисленные экспериментальные исследования, колебания экипажа на упругом пути имеют случайный характер. Сам путь находится под влиянием значительного числа случайных и нестационарных факторов. Наибольшее число воздействий сложной механической системы «путь—подвижной состав» имеют случайный характер. Поэтому наиболее полно и всесторонне исследовать поведение динамических систем можно с помощью вероятностных методов и, в частности, с помощью их новейшего раздела—теории случайных функций [66].

Рис. 2.1. Расчетная схема системы
Изучением случайных явлений, в которых случайность проявляется в форме процесса, занимается специальная отрасль теории вероятностей — теория случайных функций (теория случайных и стохастических процессов). Эту науку называют «динамикой случайных явлений» и она является сравнительно новым разделом теории вероятностей, развившемся за последние 50—60 лет.
Численное интегрирование, получившее широкое распространение при анализе динамических систем, предполагает рассмотрение развития процесса во времени. Это мощный аппарат для исследования нелинейных систем.
Но наряду с таким подходом разработаны методы исследования линейных систем, которые (учитывая особенности линейных систем) позволяют существенно упростить решение задач анализа динамических систем без потери интересующей информации, а в ряде случаев — получить дополнительную информацию об исследуемом объекте.
В частном случае при совместном использовании метода комплексных амплитуд и теории случайных функций удается проводить статистический анализ линейных динамических систем большой размерности (многомассовых, с большим количеством взаимных упругих и диссипативных связей), преобразуя систему дифференциальных уравнений в систему линейных алгебраических уравнений с комплексными коэффициентами.
Построенная в ходе решения амплитудно-частотная характеристика (АЧХ) системы позволяет сложить представление о таких свойствах системы, которые трудно проанализировать при численном интегрировании, особенно в случае многомассовых (многочастотных систем).
Задавая статистические характеристики внешнего воздействия на систему, с помощью частотных методов легко определить статистические характеристики интересующих выходных процессов системы, что при численном интегрировании очень трудоемко или вообще невозможно.
За последнее время широкое распространение получили методы обработки информации, в том числе и о поведении динамических систем, построенных на цифровом анализе, который, в свою очередь, базируется на спектральной теории и быстрых преобразованиях Фурье.
Учитывая интенсивное развитие теоретических методов и аппаратурной базы спектрального анализа, частотные методы исследования динамических систем следует признать наиболее современными и перспективными.
Методика исследования динамической системы «путь—подвижной состав» заключается в следующем: динамическая модель представляется как линейный оператор, преобразующий случайную возмущающую функцию в вектор случайных обобщенных координат, описывающих движение модели.

Система (2.1) может быть представлена в матричной форме:



Реакция системы на отдельное воздействие вида (2.6) будет:

Но для реализации приведенной методики на ЭВМ интеграл (2.12) необходимо численно вычислять в конкретном интервале частот ωϵ[0, Ω], где Ω—частота среза спектра (граничная частота, за пределами которого интеграл не вычисляется).
Эта частота определяется из того условия, что дальнейшее прибавление к уже существующей сумме, накапливаемой в диапазоне от 0 до Ω, не привнесет в значение интеграла (а точнее—суммы) дополнительного вклада, который существенно повлияет на его значения.
Иначе говоря, интеграл (2.12) должен сходиться, т. е. подынтегральная функция должна быть убывающей. И если АЧХ системы имеет ярко выраженные резонансы, то каждый резонанс должен войти в рассматриваемый диапазон частот [О, Ω]. В этом случае величину Ω целесообразно принимать в 1,2—1,7 раза выше наибольшей собственной частоты системы. В противном случае лучше пересмотреть структуру математической модели, ее расчетную схему и устранить осциллятор, порождающий высшую частоту, если она не является основной для исследуемого процесса.
Поэтому перед моделированием динамических систем целесообразно провести анализ ее собственных частот.
В подавляющем большинстве рельсовых экипажей демпфирование в упругих связях (или естественная диссипация в элементах конструкции) не оказывает сильного влияния на частотный состав системы. Поэтому процедуру вычисления собственных частот можно проводить без учета диссипативных характеристик, полагая, что при этом не будет внесена существенная погрешность.
В этом случае, используя инерционную и жесткостную матрицы системы, запишем уравнение для определения собственных частот и форм колебаний [69]:
![]() (2.15)
(2.15)
На сегодняшний день существуют апробированные методы решения матричного уравнения (2.15) на ЭВМ. Поэтому, не останавливаясь на теоретических основах этих методов, можно отметить, что точное значение собственных частот системы не имеет принципиального значения. Это важно лишь для определения границ исследуемого частотного диапазона. Вместе с тем, не прибегая к помощи сложных алгоритмов, первичную информацию о частотном спектре системы можно получить на основе вычисления парциальных частот. Эти частоты вычисляются в предположении, что все недиагональные элементы жесткостной матрицы равны 0. Тогда матричное уравнение (2.15) распадается на независимые уравнения для определения каждой парциальной частоты [69].
Достоверность результатов, полученных математическим моделированием, существенно зависит как от правильного выбора структуры
модели и ее параметров, так и от того, насколько корректно и точно сформулировано внешнее возмущение η(t) или его спектральная плотность Sη (ω) для исследуемого частотного диапазона.
В данном случае спектральная плотность представлена в виде [70]:
![]()
(2.16)
и учитывает следующие компоненты:
—периодически повторяющиеся стыковые неровности (i = 1);
- неровности рельсового звена (i = 2);
—микромакронеровности пути (i = 3);
- неровности колес (i = 4).
Стыковая неровность представлена в виде периодически повторяющихся равноотстоящих импульсов одинаковой формы, но различной амплитуды и длительности. Так как временной интервал θ0 между характерными точками соседних стыков велик по сравнению с длительностью τ0 импульса на стыке, а плотность вероятности распределения амплитуды импульсов нормальная, получим выражение спектральной плотности указанной последовательности импульсов:
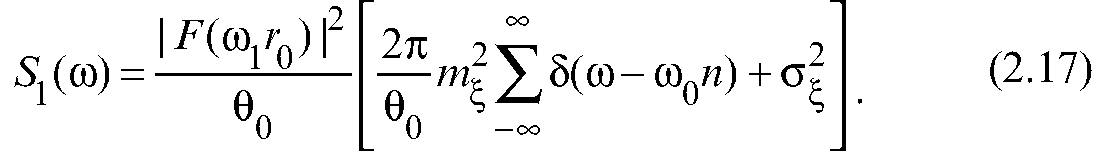
Как следует из выражение (2.17), спектральная плотность состоит из непрерывного спектра и дискретных спектральных линий, расположенных друг от друга на расстоянии 1/θ0. Форма непрерывного спектра такая же, как форма спектра Ρ(ω, τ0) отдельного импульса. Огибающая спектральных линий такая же, как и огибающая непрерывного спектра и зависит от спектра отдельного импульса.
Учитывая, что неровности пути на стыках имеют различную форму, логично в качестве исходной взять неровность, дающую монотонно убывающий спектр. Такой спектр имеет импульс гауссовской формы (рис. 2.2), математическое ожидание которого во временной области определяется выражением:
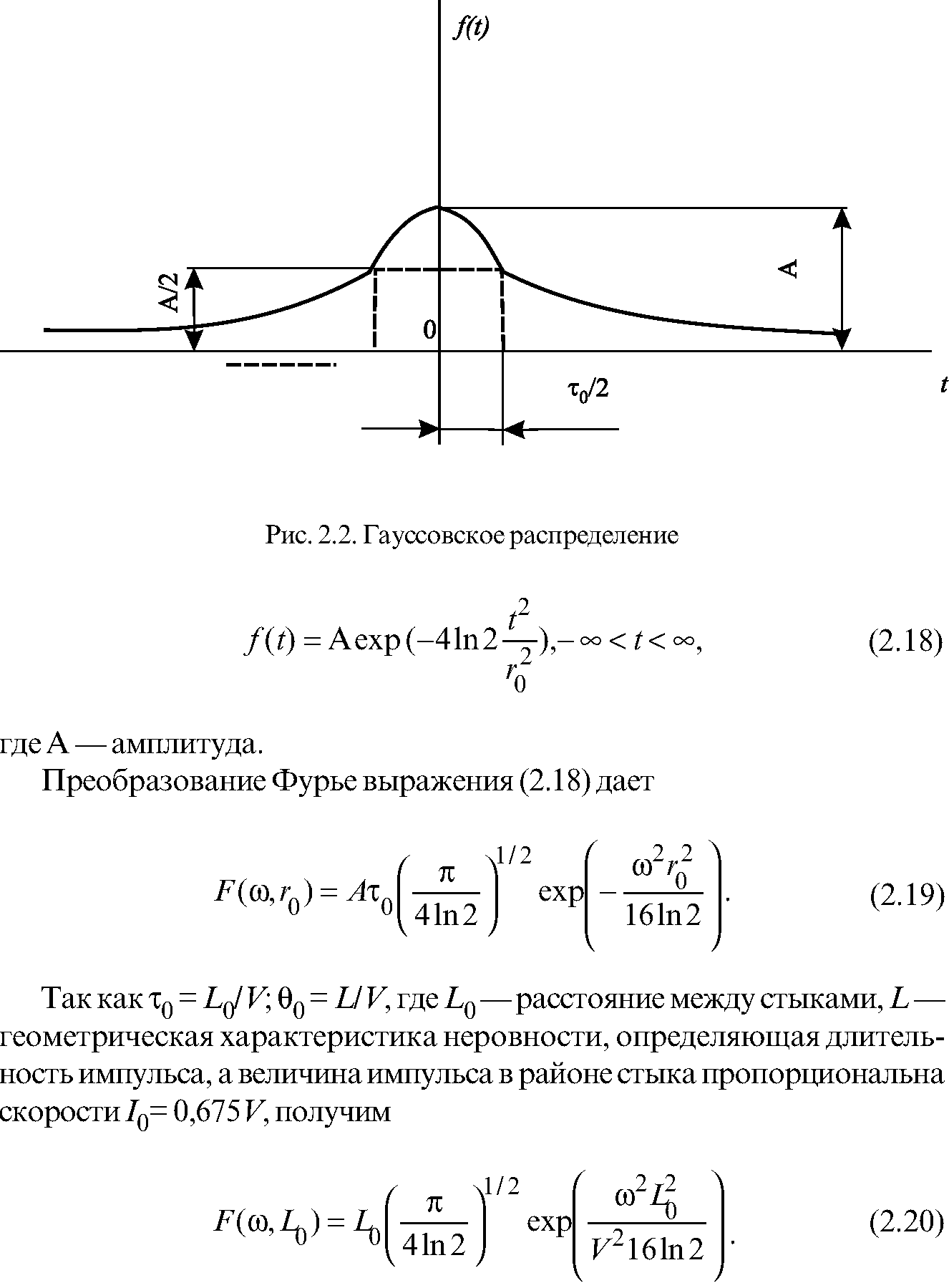
Аналитическое выражение спектральной плотности возмущений от рельсового звена рекомендуется принимать [69] в форме:
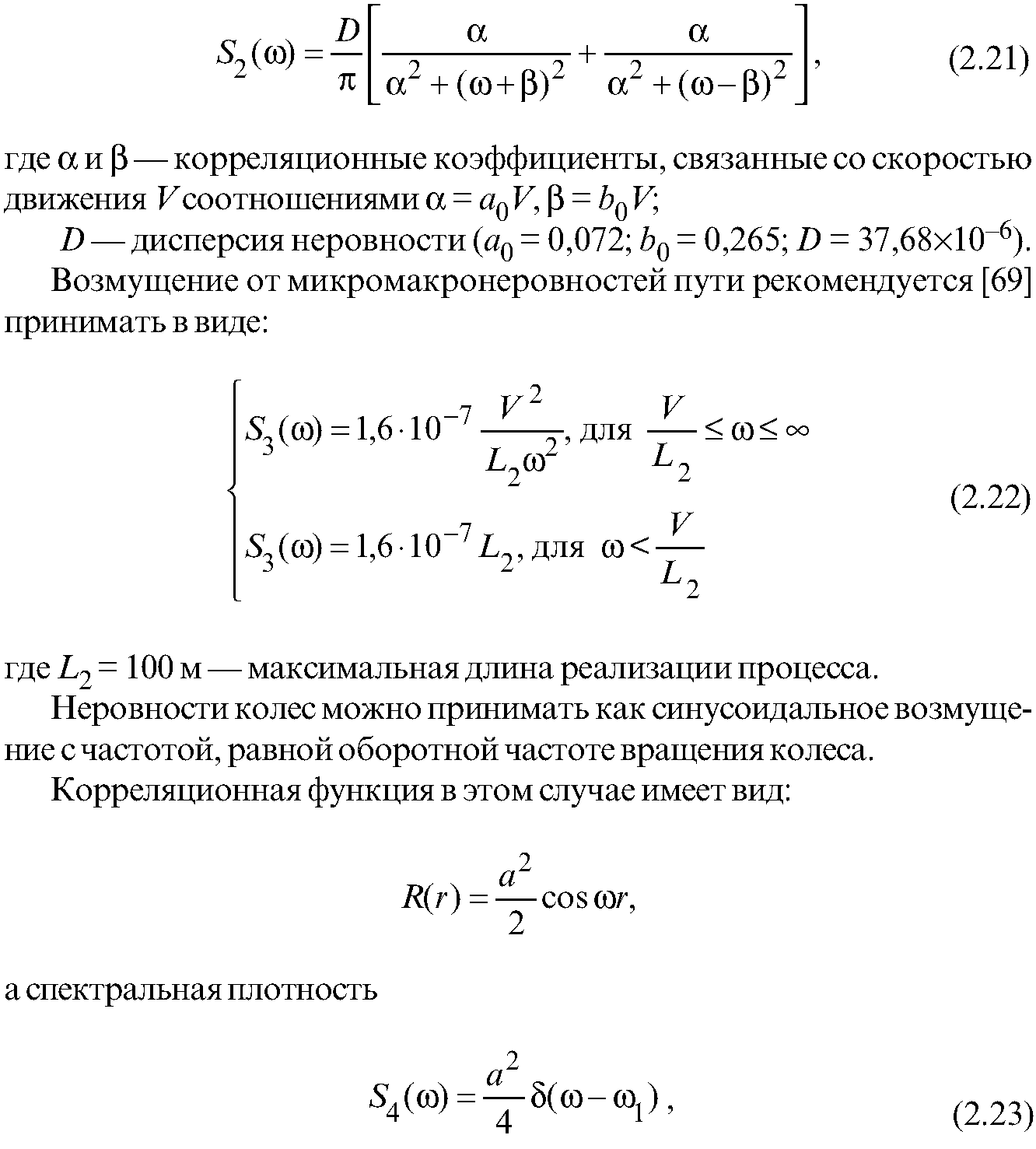
где а—амплитуда неровности на колесе; ω1—циклическая частота вращения колеса.
Анализируя выражения (2.17)—(2.23), можно обобщить особенности задаваемого возмущения: возмущающий спектр содержит как сплошную, так и дискретные составляющие, задаваемые дельта-функциями Дирака.
При этом дискретные составляющие сосредоточены в низкочастотной части спектра (от 0 до 10 Гц).
Сплошные компоненты по выражениям (2.21) и (2.22) аппроксимируются функциями, удовлетворительно отражающими физический смысл процессов в низкочастотной области. Использование этих функций для исследований в высокочастотном диапазоне неприемлемо: степень их убывания (пропорционально 1/ω2) для верной интерпретации высокочастотного взаимодействия элементов системы недостаточна.
Вместе с тем имеются экспериментальные данные о спектральных плотностях высокочастотных процессов.
В частности, в работе [71] предлагается аналитическая зависимость, описывающая возмущающий спектр, характерный для высокочастотных (до 1000 Гц) динамических процессов при взаимодействии экипажа и пути:

Для удобства реализации описанной выше методики на ЭВМ (вычисление АЧХ, задание спектральной плотности возмущения, вычисление определенного интеграла и пр.) желательно иметь постоянный шаг по частоте ω. С этой целью удобно аппроксимировать набор дискретных низкочастотных составляющих спектра сплошной составляющей с ярко выраженными узкополосными «всплесками» в области частот, равных частотам дискретных составляющих.
Для такой аппроксимации вполне подходит выражение вида [71]:
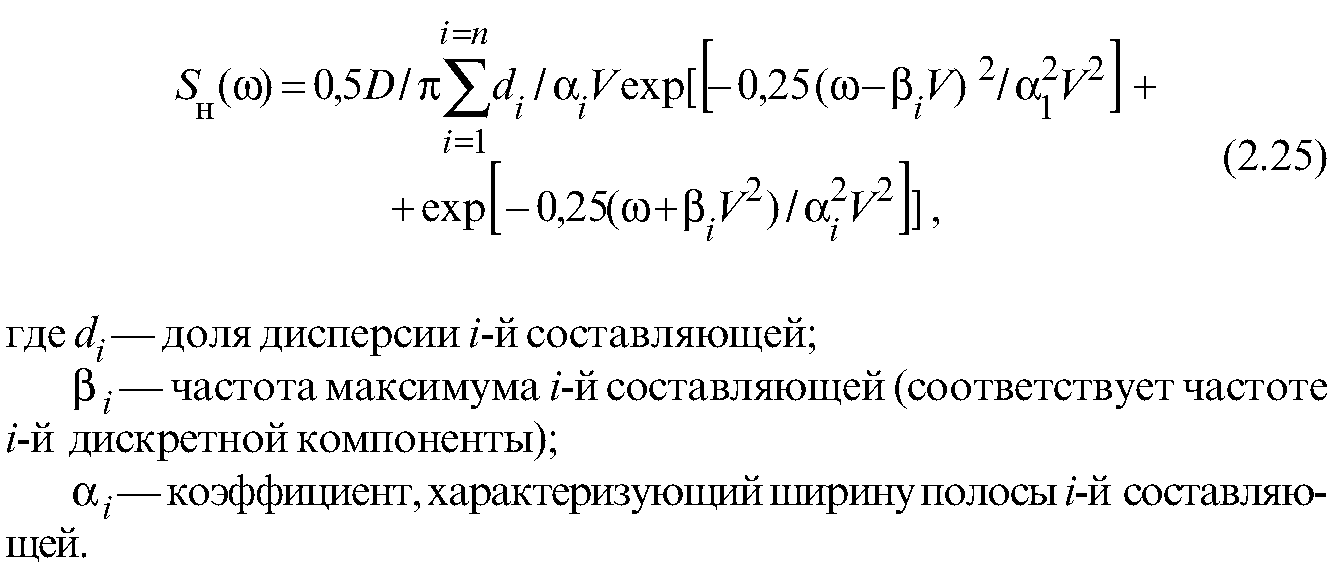
Таким образом, возмущающий спектр, сформированный с учетом выражений (2.24) и (2.25) в виде:
![]()
(2.26)
отражает периодические свойства неровностей пути как в области низких, так и высоких частот (рис. 2.3).

Рис. 2.3. Спектральная плотность возмущения Sη(ω) (начало): а — гармоника стыка; б — полный спектр до 60 Гц
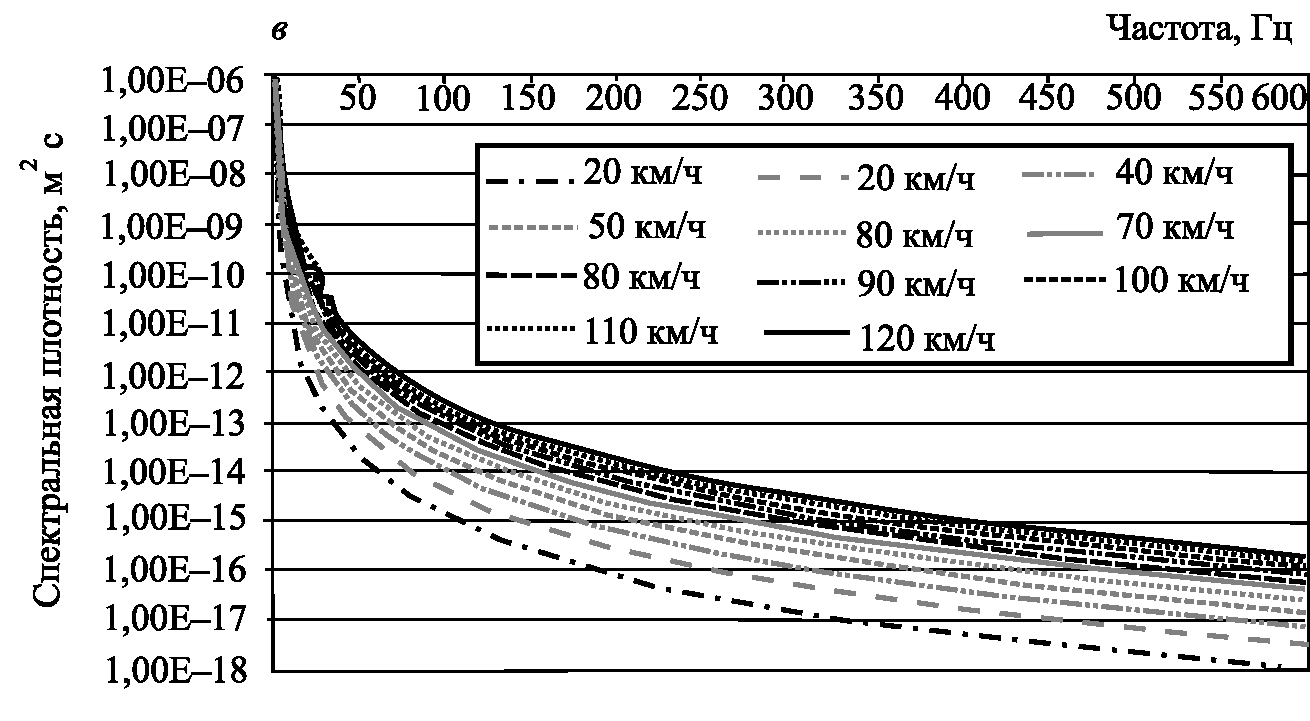
Рис. 2.3. Спектральная плотность возмущения Sη(ω) (окончание): в — полный спектр до 600 Гц
