Глава 3. ЧИСЛЕННЫЕ МЕТОДЫ ТЕОРИИ ОПТИМИЗАЦИИ
- Методологические основы оптимизации и постановка задачи
Оптимизация — процесс выбора наилучшего варианта из возможных, либо процесс приведения системы в наилучшее (оптимальное) состояние.
Эффективность оптимизационных методов, позволяющих осуществить выбор наилучшего варианта без непосредственной проверки всех вариантов, тесно связана с широким использованием достижений в области математики. Она (эффективность) достигается путем реализации итеративных вычислительных схем, опирающихся на строго обоснованные логические процедуры.
Так как размерность инженерных задач, как правило, очень велика, а расчеты по оптимизационным алгоритмам требуют значительных затрат времени, оптимизационные методы ориентированы главным образом на реализацию с помощью ЭВМ.
Для того чтобы использовать численные методы теории оптимизации для решения конкретной инженерной задачи, необходимо установить границы инженерной системы, подлежащей оптимизации, определить количественный критерий, на основе которого можно провести анализ всех возможных вариантов с целью выявления лучшего, осуществить выбор параметров, которые используются для определения характеристик и идентификации вариантов и в конечном счете построить модель, отражающую взаимосвязи между параметрами-переменными.
Эта последовательность действий составляет суть процесса инженерной оптимизации.
Корректная постановка задачи служит ключом к успеху оптимизационного исследования и является в большей степени искусством, нежели точной наукой.
Искусство постановки задач постигается в практической деятельности на примерах успешно реализованных разработок и основывается на четком представлении преимуществ, недостатков и специфических особенностей различных методов теории оптимизации.
Прежде чем приступить к оптимизационному исследованию, необходимо четко определить границы изучаемой системы. В большинстве конкретных инженерных задач изучаемая система предстает как некоторая изолированная часть реального мира. Границы системы задаются пределами, отделяющими систему от внешней среды, и служат для ее выделения из окружения. При проведении анализа обычно предполагается, что взаимосвязи между системой и внешней средой зафиксированы на некотором заранее определенном уровне представления. Поскольку такие связи всегда существуют, определение границ системы является первым шагом в процессе ее приближенного описания.
В ряде случаев может оказаться, что первоначальный выбор границ системы является слишком жестким, для более полного анализа может возникнуть необходимость расширения этих границ. В этом случае в изучаемую инженерную систему включаются подсистемы, оказывающие существенное влияние на ее функционирование.
Расширение границ системы повышает ее размерность. Она становится многокомпонентной и значительно усложняется, что в значительной мере затрудняет ее анализ. Очевидно, что на практике следует, насколько это возможно, стремиться к разбиению больших сложных систем на относительно небольшие подсистемы, которые можно изучать в отдельности. Однако при этом необходимо быть уверенным в том, что такая декомпозиция не приведет к излишнему упрощению системы реальной.
Если подлежащая исследованию система определена и ее границы установлены, то на следующем этапе постановки оптимизационной задачи необходимо осуществить выбор критерия, на основе которого можно оценить характеристики проекта, с тем чтобы выявить наилучшее из множества лучших условий ее функционирования. Спектр возможных формулировок таких критериев довольно широк и зависит от типа инженерного приложения. Независимо от того, какой критерий выбирается при оптимизации, наилучшему варианту всегда соответствует минимальное или максимальное значение характеристического показателя качества функционирования системы.
Необходимо точно представлять себе, что независимо от содержания оптимизационного метода, только один критерий может быть использован при определении оптимума, так как невозможно получить решение, которое одновременно обеспечивало минимум затрат на реализацию проекта, максимум надежности и минимум потребляемой энергии. Здесь мы опять сталкиваемся с упрощением реальной ситуации, так как в ряде инженерных задач было бы весьма желательным найти решение, которое явилось бы наилучшим с позиций нескольких различных критериев.
Одним из способов учета противоречивости нескольких критериев состоит в том, что какая-либо характеристическая мера выбирается в качестве первичной, тогда как остальные считаются вторичными. В этом случае первичный критерий используется при оптимизации в качестве целевой функции, а вторичные порождают ограничения оптимизационной задачи, устанавливая диапазоны изменения соответствующих показателей от максимального до минимального значения.
За последние годы разработан ряд методов решения мультикритериальных оптимизационных задач различных типов, однако, освещению этого нового и постоянно совершенствующегося сложного аналитического аппарата должна быть посвящена отдельная работа.
На следующем, основном, этапе постановки задачи необходимо выбрать независимые переменные, которые адекватно описывают допустимые проекты или условия функционирования исследуемой системы.
В процессе выбора переменных необходимо учесть ряд важных факторов. Во-первых, необходимо провести различие между переменными, значения которых могут изменяться в достаточно широких пределах и переменными, значения которых фиксированы и определяются внешними факторами. Далее необходимо провести различие между теми параметрами системы, которые могут предполагаться постоянными, и параметрами, которые подвержены изменениям вследствие воздействия внешних или неконтролируемых факторов. Во-вторых, при постановке задачи следует учитывать все основные переменные, которые влияют на функционирование системы или качество проекта. Независимые переменные должны выбираться таким образом, чтобы все важнейшие технико-экономические решения нашли отражение в формулировке задачи. Исключение возможных альтернатив может привести к получению субоптимальных решений.
Еще одним существенным фактором, влияющим на выбор переменных при постановке задачи, является уровень детализации при исследовании системы. Очень важно ввести в рассмотрения все основные независимые переменные, но не менее важно не перегружать задачу большим количеством мелких, несущественных деталей. При выборе независимых переменных целесообразно руководствоваться правилом, согласно которому следует рассматривать только те переменные, которые оказывают существенное влияние на характеристический критерий, выбранный для анализа сложной системы.
После выбора характеристического критерия и независимых переменных необходимо построить модель, которая описывает взаимосвязи между переменными и отражает влияние независимых переменных на степень достижения цели.
На самом нижнем микроуровне математические модели представлены в виде дифференциальных уравнений в частных производных с граничными условиями. К этим моделям, называемым распределенными, относятся многие уравнения математической физики. Объектами исследований здесь являются физические величины, что требуется при анализе прочности строительных конструкций, исследовании процессов в жидких средах, моделировании концентраций и потоков частиц в электронных приборах и т. п.
Число совместно исследуемых различных сред (число деталей, слоев материала, фаз агрегатного состояния) в практических моделях микроуровня не может быть большим ввиду сложностей вычислительного характера. Резко снизить вычислительные затраты в многокомпонентных средах можно только, если применить иной подход к моделированию, основанный на принятии некоторых допущений.
Допущение, выражаемое дискретизацией пространства, позволяет перейти к моделям на макроуровне. Моделями макроуровня, называемыми также сосредоточенными, являются системы алгебраических и дифференциальных уравнений, поскольку независимой переменной здесь остается только время. Упрощение описания отдельных компонентов (деталей) позволяет исследовать модели процессов в устройствах, приборах, механических узлах, число компонентов в которых может доходить до нескольких тысяч.
В тех случаях, когда число компонентов в исследуемой системе превышает некоторый порог, сложность такой модели на макроуровне снова становится чрезмерной. Поэтому, принимая соответствующие допущения, переходят на функционально-логический уровень. На этом уровне используют аппарат передаточных функций, если объектом исследований является аналоговый процесс, элементы математической логики и теории конечных автоматов, если объектом исследования является процесс дискретный.
Наконец, для исследования еще более сложных объектов, примерами которых является деятельность предприятий и их объединений, вычислительных систем и сетей, социальных систем и других подобных объектов, применяют аппарат теории массового обслуживания, возможно использование и некоторых других подходов, например сетевых. Эти модели относятся к системному уровню моделирования.
Основными требованиями к модели являются требования адекватности, точности, экономичности.
Модель всегда лишь приближенно отражает некоторые свойства объекта. Адекватность имеет место, если модель отражает заданные свойства объекта с требуемой точностью. Под точностью понимают степень соответствия оценок одноименных свойств объекта и модели.
Адекватность оценивается перечнем отражаемых свойств и областями адекватности. Областью адекватности называется совокупность параметров, в пределах значений которых погрешности модели остаются в допустимых пределах. Например, областью адекватности модели радиоэлемента будет диапазоны изменения моделируемых температур, внешних напряжений, частот.
Экономичность (вычислительная эффективность) определяет затраты ресурсов, необходимых для реализации модели. Поскольку реализация математических моделей предполагает использование ЭВМ, под эффективностью понимаются затраты машинного времени и памяти.
Аналогичные требования по точности и экономичности предъявляются при выборе численных методов решения уравнений, описывающих поведение модели.
В качестве примеров компонентных и топологических уравнений, описывающих поведение электрических систем на макроуровне можно привести законы Ома и Кирхгофа в дифференциальной форме.
В электрических системах переменными являются электрическое напряжение и токи. Компонентами систем могут быть простые двухполюсные элементы и более сложные, многополюсные. К простым двухполюсным относятся физические величины, известные вам еще со школы: сопротивление, емкость, индуктивность. В эквивалентных схемах эти элементы обозначают соответственно R, С, L.
Тогда компонентные уравнения простых двухполюсников будут иметь вид:

По аналогии с электрическими системами можно составить компонентные и топологические уравнения, описывающие поведение механической системы.
Фазовыми переменными в механических системах являются силы и скорости. Используют одну из двух возможных электрических аналогий. Мы используем ту из них, где скорость относят к фазовым переменным типа потенциала, а силу считают фазовой переменной типа потока. Учитывая формальный характер этих аналогий, в равной степени правомерно будет применить и противоположную аналогию.
Компонентные уравнения характеризуют инерционные свойства тел и имеют вид (второй закон Ньютона):

Топологические уравнения характеризуют:
1. Закон равновесия сил: сумма всех сил, приложенных к телу, включая силу инерции равна нулю (закон Даламбера);

Рис. 3.1. Условные обозначения простых элементов в эквивалентных схемах
2. Закон скоростей, согласно которому сумма относительной, переносной и абсолютной скоростей равна нулю.
В механических вращательных системах справедливы компонентные и топологические уравнения поступательных систем с заменой поступательных систем на угловые, сил—на вращательные моменты, масс—на моменты инерции, жесткости—на вращательные жесткости.
На рис. 3.1 представлены условные обозначения простых элементов в эквивалентных схемах.
Нетрудно заметить аналогию между компонентными и топологическими уравнениями электрической и механической систем. Так, токам и напряжениям соответствуют силы или моменты инерции и скорости механической системы, компонентным уравнениям (см. рис. 3.1) и фигурирующим в них параметрам C,L,U—уравнения и параметры М, U, LM. Параметры С и М называются емкостными, параметры — индуктивными, а параметры R и Rтp=dU/dF— резистивными.
Однако имеется существенное отличие в моделировании электрических и механических систем: первые из них одномерны, процессы в механических системах часто приходится рассматривать в двумерном или даже в трехмерном виде. Это означает, что в случае трехмерного представления фазовые переменные представляются в векторной форме, каждая имеет шесть компонентов, соответствующих шести степеням свободы.
Однако отмеченные выше аналогии остаются справедливыми, если их относить к проекциям сил и скоростей на пространственные оси, а при графическом представлении моделей использовать шесть эквивалентных схем—три для поступательной модели, три для вращательной.

Рис. 3.2. Тележка:
А — платформа; В1, В2 — колеса; С1, С2—рессоры
Известен ряд методов формирования ММС на макроуровне. Получаемые с их помощью модели ориентированы на те или иные численные решения и различаются набором базисных параметров, т. е. фазовых переменных, остающихся в уравнениях итоговой ММС. Общей для всех методов является исходная совокупность топологических и компонентных уравнений.
При записи топологических уравнений удобно использовать промежуточную графическую форму — представление модели в виде эквивалентной схемы. Если речь идет о моделировании трехмерной механической системы, то для каждой степени свободы строят свою эквивалентную схему.
В качестве примера на рис. 3.2 изображена некоторая механическая система, тележка, движущаяся по дороге и состоящая из платформы А, колес В1, В2 и рессор С1, С2. На рис. 3.3 приведена эквивалентная схема для вертикальных составляющих сил и скоростей, на которой телам системы соответствуют одноименные узлы, учитываются массы платформ и колес, упругость рессор, трение между колесами и дорогой. Неровности дороги вызывают источниками силы воздействие на систему.
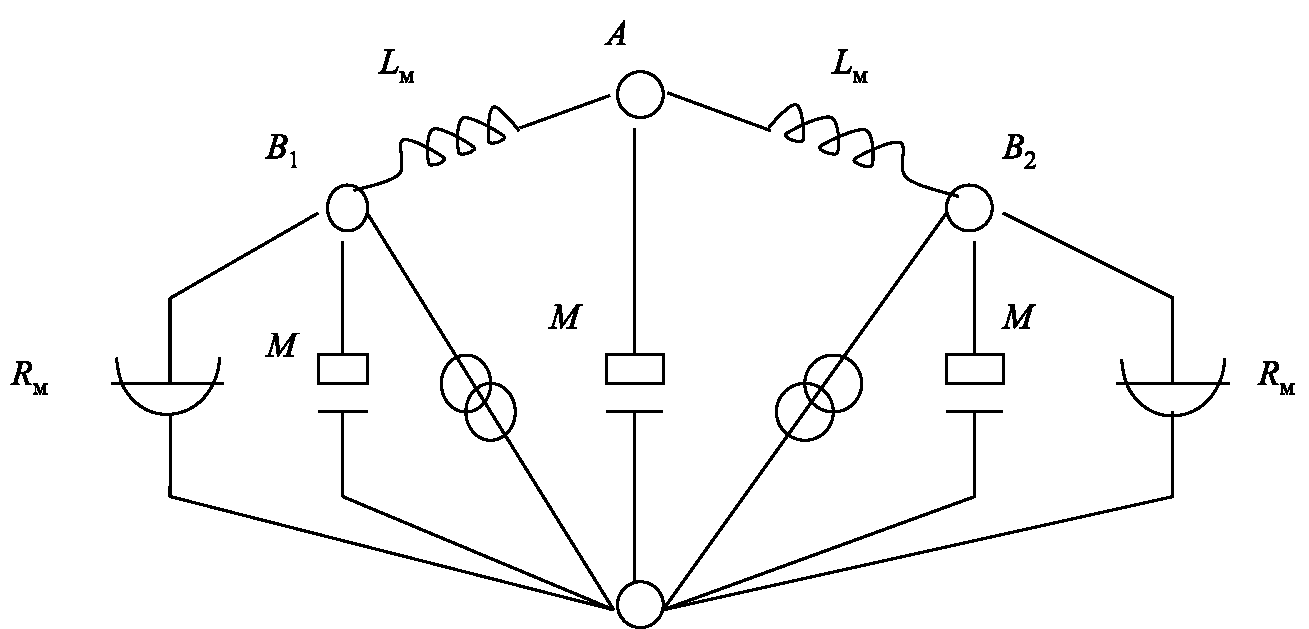
Рис. 3.3. Эквивалентная схема
В принципе оптимизационное исследование можно провести непосредственно экспериментируя с реальной системой. Для этого следует зафиксировать значения независимых внутрисистемных переменных, реализовать процедуру наблюдения за функционированием системы в этих условиях и оценить значение характеристического показателя качества функционирования системы, исходя из зарегистрированных характеристик. Затем с помощью оптимизационных методов можно скорректировать значения независимых переменных и продолжить серию экспериментов. Однако на практике оптимизационное исследование с помощью построения модели является более предпочтительным, так как эксперименты с реальными системами обычно требуют слишком больших затрат времени и средств, а также в ряде случаев оказываются связаны с риском.
Очевидно, что процесс построения модели является весьма трудоемким и требует четкого понимания специфических особенностей рассматриваемой системы.
Из всего сказанного следует, что задача в виде, пригодном для оптимизационных методов, включает в себя характеристическую меру, множество независимых переменных и модель, отражающую их взаимосвязь. Область применения методов оптимизации достаточно широка, так как требования, предъявляемые к оптимизационным задачам, являются весьма общими и носят абстрактный характер.
