Улучшение взаимодействия пути и состава - Обзор существующих методов оптимизации

Несмотря на то что методы теории оптимизации отличаются универсальностью, их успешное применение в значительной степени зависит от профессиональной подготовки инженера, который должен иметь четкое представление о специфических особенностях изучаемой системы. Для того, чтобы использовать методы оптимизации необходимо разработать принципиальную схему функционирования системы или выявить ее структуру. Тогда задача оптимизации сведется к выбору таких значений переменных, которым соответствует наилучшее значение целевой функции.

называется задачей оптимизации с ограничениями или задачей условной оптимизации. Задача, в которой нет ограничений, т. е.

называется оптимизационной задачей без ограничений или задачей безусловной оптимизации.
Задачи оптимизации можно классифицировать в соответствии с видом функций и размерностью вектора. Задачи без ограничений, которые представляют собой одномерный вектор, называются задачами с одной переменной и составляют простейший, но весьма важный подкласс оптимизационных задач.
Задачи условной оптимизации, в которых функции hk и gj линейны, являются линейными и называются задачами с линейными ограничениями. В таких задачах целевые функции могут быть линейными, либо нелинейными. Задачи, которые содержат только линейные функции вектора, называются задачами линейного программирования, в задачах целочисленного программирования компоненты вектора должны принимать только целые значения.
Задачи с нелинейной целевой функцией и линейными ограничениями иногда называют задачами нелинейного программирования с линейными ограничениями. Оптимизационные задачи такого рода можно классифицировать на основе структурных особенностей нелинейных целевых функций. Если f(x)—квадратичная функция, то мы имеем дело с задачей квадратичного программирования, если f(x)—дробнолинейная функция, то соответствующая задача носит название дробно-линейного программирования и т.д. Деление оптимизационных задач на такие классы представляет значительный интерес, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов их решения.
Учитывая все сказанное, методы оптимизации можно классифицировать по ряду признаков, представленных в табл. 3.1.

Таблица 3.1
Классификация методов оптимизации

Основные методы оптимизации, применяемые при решении инженерных задач — методы поисковые. Сущность метода заключается в том, что на каждом шаге оптимизации управляемые параметры изменяются на величину некоторого приращения. Это приращение вычисляется по формуле и зависит от значения самого управляемого параметра, от направления поиска и от шага итерации, который задается заранее.

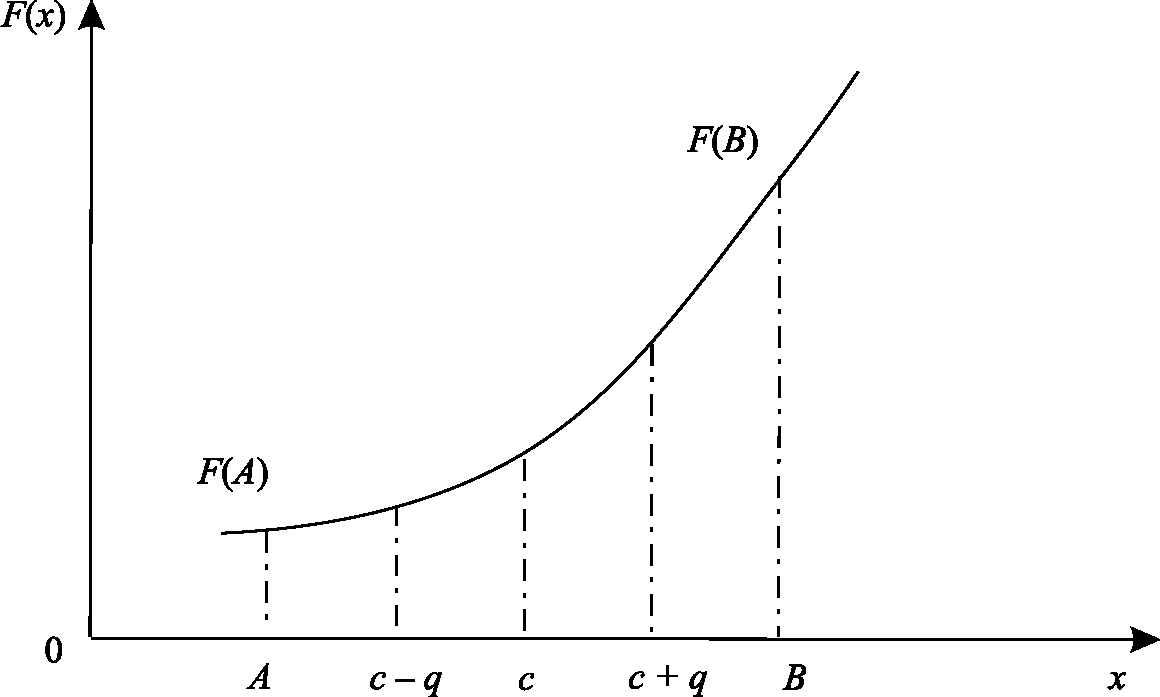
Рис. 3.4. Метод дихотомического деления

Методы одномерной оптимизации играют вспомогательную роль на отдельных этапах многомерного поиска.
Для реальных задач характерно наличие ограничений, однако методы условной оптимизации с помощью специальных методов сводят к задачам без ограничений.
Методы глобального поиска, удовлетворительные по вычислительной эффективности для общего случая отсутствуют, поэтому на практике используют методы поиска локальных экстремумов.
Методы первого порядка производных называются также градиентными, так как вектор первых производных целевой функции по управляемому параметру есть градиент целевой функции.
К методам одномерной оптимизации относятся методы дихотомического деления, золотого сечения, чисел Фибоначчи, полиноминальной аппроксимации и их модификации.

Таким образом, на следующем шаге для поиска экстремума выбирается суженный отрезок. Шаги повторяются, пока длина шага не станет равной величине погрешности q.

1. Метод золотого сечения. Похож на метод дихотомического деления (см. рис. 3.5).
2. Метод Фибоначчи. Используется ряд чисел Фибоначчи. Метод аналогичен методу золотого сечения с тем отличием, что начальное значение i определяется из условия, что Ri должно быть наименьшим числом Фибоначчи, превышающим величину (В-А)/Е (где Е—заданная допустимая погрешность определения экстремума).
3. В методах полиноминальной аппроксимации целевая функция представляется квадратичным полиномом

Коэффициенты αi - определяют путем решения системы алгебраических уравнений, которую составляют, вычисляя значения целевой функции в известных точках.
К методам полиноминальной аппроксимации тесно примыкает метод последовательного оценивания с использованием квадратичной

аппроксимации, разработанный Пауэллом [72]. Метод основан на последовательном применении процедуры оценивания с использованием квадратичного полинома. Схему алгоритма можно описать следующим образом. Пусть х1 — начальная точка, ∆х—выбранная величина шага по оси х, тогда последовательно:  

Рис. 3.6. Метод Ньютона—Рафсона

Рис. 3.7. Метод Ньютона—Рафсона

Приравнивая правую часть уравнения (3.1) к нулю, получим следующее приближение:

Затем перейти к шагу 3.
Шаги 1 и 2 реализуют процедуру поиска границ интервала по эвристическому методу, прочес изменения знака производной используется в качестве критерия перехода через точку минимума. На шаге 3 производится вычисление координаты точки оптимума аппроксимирующего полинома. На шаге 4 проверяется факт того, что полученная оценка действительно является улучшенным приближением к точке оптимума. В случае, когда значения производной вычисляются непосредственно, метод поиска с использованием кубичной аппроксимации, безусловно, оказывается более эффективным по сравнению с любым из представленных выше методов. Однако, если значения производной вычисляются путем разностного дифференцирования, то предпочтение следует отдать методу Пауэлла, основанному на квадратичной аппроксимации.
С помощью теоретических выкладок можно показать, что такие методы точечного оценивания, как метод Пауэлла или метод поиска с использованием кубичной аппроксимации и производных, существенно эффективнее методов исключения интервалов, среди которых выделяется метод золотого сечения. В частности известно, что применение метода поиска с использованием квадратичной аппроксимации позволяет достигнуть асимптотически суперлинейной скорости сходимости к точке истинного минимума, т. е. отклонение к + 1-й оценки от истинной координаты точки минимума пропорционально отклонению к-й оценки, возведенному в степень α>1 (как показано в [72] α =1,3). Для сравнения отметим, что если при реализации метода золотого сечения в качестве к-й оценки координаты точки истинного минимума берется координата средней точки интервала, полученного в результате вычислений значения функции, то отклонение этой оценки от точной координаты линейно убывает при переходе от к к к+1-й итерации. Это означает, что в случае, когда интервалы сходимости сравнимы между собой, метод, основанный на квадратичной аппроксимации, сходится быстрее, чем любой из методов исключения интервалов. Разумеется, сделанный вывод справедлив лишь в предположении, что интервалы сходимости сравнимы между собой, а исследуемая функция является достаточно гладкой и унимодальной.
Результаты численных экспериментов, представленных в специальной литературе, не подтверждают преимущество методов с использованием производных и квадратичной аппроксимации или метода исключения интервалов над остальными методами. Если для вычисления значений целевой функции требуется значительное машинное время, то, по мнению авторов работы [73], предпочтительнее использовать стратегию поиска, основанную на модификации метода Пауэла. Это мнение подтверждается результатами вычислительных экспериментов, проведенных Химмельблау [74], который сравнил указанную стратегию поиска со схемой поиска по золотому сечению и показал, что модифицированный метод Пауэлла требует меньшего количества вычислений значений функции для достижения заданной точности при оценивании координаты точки минимума.
Если необходимо получить решение с очень высокой степенью точности, то лучшими оказываются методы поиска на основе полиноминальной аппроксимации. С другой стороны, известно, что при исследовании мультимодальных или быстро изменяющихся функций метод Пауэлла сходится значительно медленнее, чем методы исключения интервалов. Таким образом, если очень важно добиться надежной работы алгоритма, то целесообразно выбрать метод золотого сечения. Поэтому поисковые методы типа метода Пауэлла следует использовать совместно с методом золотого сечения, переход к алгоритму которого осуществляется в тех случаях, когда реализации соответствующих итераций на ЭВМ связаны с определенными трудностями.
Одномерные методы оптимизации играют весьма важную роль при исследовании функций нескольких переменных. При этом вопрос поиска точек оптимума многомерной функции рассматривается с использованием положений линейной алгебры и дифференциального исчисления. Задача выбора указанных точек остается вне рамок проводимого анализа, так как основное внимание уделяется решению вопроса о том, соответствуют ли исследуемые точки решениям многомерной задачи безусловной оптимизации, в которой требуется минимизировать f(х), при отсутствии ограничений на х, где х — вектор управляемых переменных размерности.
— скалярная целевая функция. 
Обычно предполагается, что хi, i = 1,2...n могут принимать любые значения, хотя в ряде практических приложений область значений выбирается в виде дискретного множества. Кроме того, часто оказывается удобным
предполагать, что функция f(х) и ее производные существуют и непрерывны всюду, хотя известно, что оптимумы могут достигаться в точках разрыва f(х) или ее градиента:

Методы, ориентированные на решение задач безусловной оптимизации, можно разделить на три широких класса в соответствии с типом информации, используемой при реализации того или иного метода:

1. Методы прямого поиска, основанные на вычислении значения только целевой функции;
2. Градиентные методы, в которых используются точные значения первых производных f(х);
3. Методы второго порядка, в которых наряду с первыми производными используются также вторые производные функции f(х).

Ни один из этих методов или их вышеперечисленных классов методов не отличается высокой эффективностью при решении оптимизационных задач различных типов. В частности, возможны случаи, когда происходит переполнение памяти ЭВМ; в других ситуациях, вычисление целевой функции требует непомерных затрат машинного времени; в некоторых задачах требуется получить значения с очень высокой степенью точности. В ряде приложений либо вообще невозможно, либо весьма затруднительно получить аналитическое выражение для производных целевой функции. Поэтому, если предполагается использовать градиентные методы, следует применить процедуру разностной аппроксимации производных. В свою очередь это приводит к необходимости экспериментального определения длины шагов, позволяющего определить надлежащее соответствие между ошибкой округления или ошибкой аппроксимации. Таким образом, инженер вынужден приспосабливать применяемый метод к конкретным характеристикам решаемой задачи.
Методы решения задач нелинейной оптимизации отличаются относительно высоким уровнем развития по сравнению с другими методами нелинейного программирования. В специальной литературе представлены достаточно полные обзоры таких методов. Отличным примером такого обзора может служить книга Мюррея [75]. К методам нелинейного программирования относятся методы прямого поиска, для реализации которых требуются только значения целевой функции, градиентные методы и методы второго порядка. Предполагается, что функция непрерывна, может как существовать, так и не существовать. Однако методы прямого поиска можно применять для решения задач, когда Vf существует, и они часто используются в тех случаях, когда Vf представляет собой сложную векторную функцию управляемых переменных. Если же эти методы применяются для анализа мультимодальных функций, то приходится ограничиваться идентификацией локальных экстремумов.
Многомерные методы, реализующие процедуру поиска оптимума на основе вычисления значений функции, можно разделить на эвристические и теоретические. Эвристические методы реализуют процедуру поиска с помощью интуитивных геометрических представлений и обеспечивают получение частных эмпирических результатов. Теоретические методы основаны на фундаментальных математических теоремах и обладают такими определенными свойствами, как сходимость, по крайней мере, при выполнении определенных условий. Ниже рассматриваются три метода прямого поиска:

1. Поиск по симплексу или S2-метод.
2. Метод поиска Хука—Дживса.
3. Метод сопряженных направлений Пауэлла.

Первые два из перечисленных методов относятся к категории эвристических и реализуют принципиально различающиеся стратегии поиска. В процессе поиска по S2-методу последовательно оперируют регулярными симплексами в пространстве управляемых переменных, при реализации же алгоритма Хука—Дживса используется фиксированное множество координатных направлений, выбираемых рекурсивным способом. Метод Пауэлла основан на теоретических результатах и ориентирован на решение задач с квадратичными целевыми функциями. Для таких задач метод сходится за конечное число итераций. К числу общих особенностей всех трех методов следует отнести относительную простоту соответствующих вычислительных процедур, которые легко реализуются и быстро корректируются. С другой стороны, реализация этих методов часто требует гораздо более значительных затрат вычислительного времени по сравнению с градиентными методами.
Первые попытки решения задач без ограничений на основе прямого поиска связаны с использованием одномерных методов оптимизации. Как правило, при реализации таких методов допустимая область определения целевой функции заменяется дискретным множеством точек пространства управляемых переменных, а затем используются различные стратегии уменьшения области, содержащей решение задачи. Часто эта процедура оказывается эквивалентной равномерному поиску в узлах сетки, покрывающей пространство управляемых параметров, и, следовательно, непригодной для решения задач с числом переменных, превышающих 2. Более конструктивная идея заключается в выборе базовой точки и оценивания значения целевой функции в точках, окружающих базовую. Например, при решении задач с двумя переменными можно воспользоваться квадратным шаблоном (рис. 3.9). Затем «наилучшая» из пяти исследуемых точек выбирается в качестве следующей базовой точки, вокруг которой строится аналогичный образец.

Рис. 3.9. Квадратный шаблон

Если ни одна из угловых точек не имеет преимущества перед базовой, размеры шаблона следует уменьшить, после чего продолжить поиск.
Этот тип эволюционной оптимизации был использован Боксом [76] и другими исследователями для решения задач, в которых эффект варьирования значений переменных измеряется с ошибкой. В задачах большой размерности вычисление значений целевой функции проводится во всех вершинах, а также в центре тяжести гиперкуба, т. е. в точках так называемого кубического образца. Если количество переменных (размерность пространства, в котором ведется поиск), равно Ν, то поиск по кубическому образцу требует 2Ν+1 вычислений значений функции для одного образца. При увеличении размерности задачи необходимое количество вычислений значений целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.
Одна из интересных стратегий поиска решения в такой ситуации положена в основу метода поиска по симплексу, предложенного Спендли, Хекстом и Химсвортом [77]. Необходимо отметить, что указанный метод и другие подобные методы не имеют отношения к симплекс-методу линейного программирования, а сходство названий носит случайный характер.
Процедура симплексного поиска Спендли, Хекста и Химсворта базируется на том, что экспериментальным образцом, содержащим наименьшее количество точек, является регулярный симплекс. Регулярный симплекс в Х-мерном пространстве представляет собой многогранник, образованный Х+1 равноотстоящими друг от друга точками-вершинами. Например, в случае двух переменных симплексом является равносторонний треугольник, в трехмерном пространстве симплекс представляет собой тетраэдр (рис. 3.10).
В алгоритме симплексного поиска используется важное свойство симплексов, согласно которому новый симплекс можно построить на любой грани начального симплекса путем переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведенной через центр тяжести остальных вершин начального симплекса. Полученная таким образом точка является вершиной нового симплекса, а выбранная при построении вершина начального симплекса исключается. 

Рис. 3.10. Построение нового симплекса: а—начальный симплекс; б—новый симплекс

Ясно, что при таком подходе при переходе к новому симплексу требуется одно вычисление значения целевой функции. На рисунке показан процесс построения нового симплекса на плоскости.
Работа алгоритма поиска по симплексу начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой из его вершин. При этом определяется вершина, в которой целевая функция принимает наибольшее значение. Затем найденная вершина проецируется через центр тяжести остальных вершин симплекса в новую точку, которая используется в качестве вершины нового симплекса. Если функция убывает достаточно плавно, итерации продолжаются до тех пор, пока либо не будет накрыта точка минимума, либо не начнется циклическое движение по двум или более симплексам. Если вершина, которой соответствует наибольшее значение целевой функции, построена на предыдущей операции, то вместо нее берется вершина, которой соответствует следующее по величине значение целевой функции. Если некоторая вершина симплекса не исключается на протяжении более чем М итераций, то необходимо уменьшить размеры симплекса с помощью коэффициента редукции и построить новый симплекс, выбрав в качестве базовой точку, которой соответствует минимальное значение целевой функции. Спендли, Хекст и Химсворт предложили вычислить М по формуле

где N — размерность задачи, а М округляется до ближайшего целого числа. Для применения данного правила необходимо установить величину коэффициента редукции.
Поиск завершается, когда или размеры симплекса, или разности между значениями функции в вершинах становятся достаточно малыми. Чтобы пользоваться этим критерием, необходимо задать величину параметра окончания поиска.
Алгоритм S2-метода имеет несколько очевидных преимуществ:

1. Расчеты и логическая структура метода отличаются сравнительной простотой и, следовательно, соответствующая программа для ЭВМ оказывается относительно короткой;
2. Уровень требований к объему памяти ЭВМ невысокий, массив имеет размерность (N = 1, N + 2);
3. Используется сравнительно небольшое число заранее установленных параметров: масштабный множитель а, коэффициент уменьшения множителя а, если а начинает циклическое движение по симплексу, и параметры окончания поиска;
4. Алгоритм оказывается эффективным даже в тех случаях, когда ошибка вычислений значений целевой функции велика, поскольку при его реализации оперируют наибольшими значениями функции в вершинах, а не наименьшими.

Приведенные выше факторы характеризуют метод поиска по симплексу как весьма полезный при проведении вычислений в реальном масштабе времени.
Однако алгоритм обладает рядом существенных недостатков:

1. Не исключено возникновение трудностей, связанных с масштабированием, поскольку все координаты вершин симплекса зависят от одного и того же масштабного показателя а. Чтобы обойти трудности такого рода, в практических задачах следует промасштабировать все переменные, с тем чтобы их значения были сравнимы по величине.
2. Алгоритм работает слишком медленно, так как полученная на предыдущих итерациях информация не используется для ускорения поиска.
3. Не существует простого способа расширения симплекса, не требующего пересчета значений целевой функции во всех точках образца. Таким образом, если а по какой-либо причине уменьшается, то поиск должен продолжаться с уменьшенной величиной шага.

Модифицированная процедура поиска по симплексу, разработанная Нелдером и Мидом [78], частично устраняет некоторые из этих недостатков. Хотя существующая формула для определения вершин регулярного симплекса оказывается весьма удобной при построении исходного образца:

Рис. 3.11. Растяжение и сжатие симплекса а — нормальное отражение; б—растяжение; в — сжатие; е— сжатие
138

Результаты отдельных численных экспериментов, показывают, что метод Нелдера—Мида обладает достаточной эффективностью и высокой надежностью в условиях наличия случайных возмущений и ошибок при определении целевой функции. В 1972 г. Паркинсон и Хатчинсон установили, что ориентация исходного симплекса в отличие от его

формы является существенным фактором, влияющим на процедуру поиска и предложили использовать значения параметров, брать α=2, β=0,25 и γ=2,5. Такой выбор параметров позволил обеспечить хорошую работу алгоритма при повторении последовательных растяжений симплекса.
Несмотря на то, что в методе поиска по симплексу и его модификации Нелдера—Мида основное внимание уделяется геометрическому расположению пробных точек, совершенно ясно, что основная цель построения таких точек заключается в определении направления, в котором должен вестись поиск. Расположение пробных точек влияет лишь на чувствительность направления поиска к изменениям топологических свойств целевой функции. В частности, уравнение для вычисления координат отраженной точки  четко устанавливает, что множество отраженных точек описывается вектором, определяющим некоторое направление в пространстве управляемых переменных. Остальные элементы логической структуры поиска связаны лишь с выбором такой величины шага λ, которая позволяет достигнуть заметного «улучшения» значений целевой функции.
Если же главная задача работы с образцом, составленным из пробных точек, состоит в определении направления поиска, то стратегию поиска по симплексу можно усовершенствовать путем непосредственного введения множества векторов, задающих направление поиска.
Простейший подход заключается в том, что поиск ведется на основе рекурсивного перебора на множестве направлений из произвольно заданного множества.
Элементарным примером метода, в рамках которого реализуется процедура рекурсивного перебора на множестве направлений поиска, является метод циклического изменения переменных, в соответствии с которым каждый раз меняется только одна переменная. При таком подходе множество направлений поиска выбирается в виде множества координатных направлений в пространстве управляемых переменных задачи. Вдоль каждого из координатных направлений последовательно проводится поиск точки оптимума на основе методов решения задач оптимизации с одной переменной. Если целевая функция обладает свойством сферической симметрии, такой поиск обеспечивает получение решения исходной задачи. Однако, если линии функции искривлены или растянуты, что весьма часто имеет место в возникающих на практике задачах, то итерации могут превратиться в бесконечную последовательность уменьшающихся шагов и процедура поиска становится неэффективной. Кроме того, изменение координатных направлений поиска может не только оказаться неэффективным, но и привести к отсутствию сходимости к точке локального оптимума даже при бесконечном числе итераций.
Конструктивные попытки повышения эффективности этого метода были связаны с тем обстоятельством, что поиск, периодически проводимый в направлении., позволяет существенно ускорить  сходимость. Это обстоятельство было положено в основу метода, разработанного Хуком и Дживсом [79], и являющегося одним из первых алгоритмов, в которых при определении нового направления поиска учитывается информация, полученная на предыдущих итерациях. По сути, метод Хука—Дживса представляет собой комбинацию «исследующего» поиска с циклическим изменением переменных и ускоряющего поиска по образцу с использованием определенных эвристических правил. Исследующий поиск ориентирован на выявление характера локального поведения целевой функции и определение направлений вдоль «оврагов».
Для проведения исследующего поиска необходимо задать величину шага, которая может быть различна для разных координатных направлений, и изменяться в процессе поиска. Исследующий поиск начинается в некоторой исходной точке. Если значение целевой функции в пробной точке не превышает значения целевой функции в исходной точке, то шаг поиска рассматривается как успешный. В противном случае необходимо вернуться в предыдущую точку и сделать шаг в противоположном направлении с последующей проверкой значения целевой функции. После перебора всех N-координат исследующий поиск завершается. Полученную в результате точку называют базовой точкой.
Поиск по образцу заключается в реализации одного единственного шага из полученной базовой точки вдоль прямой, соединяющей эту точку с предыдущей базовой точкой. Новая точка образца определяется в соответствии с формулой

Как только движение по образцу не приводит к уменьшению целевой функции, точка фиксируется в качестве временной базовой
точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением целевой функции, чем в точке, то она рассматривается как новая базовая точка. С другой стороны, если исследующий поиск неудачен, необходимо вернуться в точку  и провести исследующий поиск с целью выявления нового направления минимизации. В конечном счете возникает ситуация, когда такой поиск не приводит к успеху. В этом случае следует уменьшить величину шага путем введения некоторого множителя и возобновить исследующий поиск. Поиск завершается, когда величина шага становится достаточно малой. Последовательность точек, получаемую в процессе реализации метода, можно записать в следующем виде:

Приведенная последовательность характеризует логическую структуру метода Хука—Дживса.
Из всего сказанного следует, что метод Хука—Дживса характеризуется несложной стратегией поиска, относительной простотой вычислений и невысоким уровнем требований к объему памяти ЭВМ, который оказывается даже ниже, чем в случае поиска по симплексу. Благодаря этому алгоритм Хука—Дживса находит широкое применение во всех областях инженерной практики, особенно эффективны его варианты с использованием штрафных функций. Однако следует отметить, что основанный на циклическом движении по координатам алгоритм в ряде случаев может заканчивать работу преждевременно, а при наличии значительных нелинейных эффектов вырождается в последовательность исследующих поисков без перехода к ускоряющему поиску по образцу.
Существует целый ряд подходов, улучшающих метод Хука—Дживса. Так, Бендлер и Макдональд [80] модифицировали процедуру Хука— Дживса путем введения дополнительных правил увеличения и уменьшения приращений переменных, а также уменьшения шага по образцу, когда обычный шаг оказывается неудачным. Эмери и О’Хаган [81] изменили фазу исследующего поиска путем введения системы ортогональных направлений, ориентация которой случайным образом меняется на каждой итерации. Розенброк [82] разработал метод, в котором, как и в
методе Хука—Дживса, новое направление поиска определяется с учетом информации, полученной на предыдущих итерациях. Однако подход, предложенный Розенброком основан на изменении множества векторов, используемых при исследующем поиске с помощью процедуры ортогонализации. Другой метод, изложенный в работе Свенна [83] и иногда называемый методом Дэвиса—Свенна—Кемпи, опирается на стратегию поиска, подобную стратегии Розенброка. При его реализации поиск ведется не с помощью фиксированных шагов по каждому из выбранных направлений, а вдоль каждой прямой, заданной одним из направлений.
Каждый из перечисленных методов обладает рядом преимуществ перед остальными при решении задач определенного типа. Если же существует необходимость реализовать более сложный алгоритм, то предпочтение следует отдать методу сопряженных направлений Пауэлла, превосходство которого над рассмотренными эвристическими методами несомненно.
Метод, разработанный Пауэллом [84], является наиболее эффективным алгоритмом прямого поиска, в особенности его модифицированные варианты, предложенные Зангвиллом [85] и Брентом [86].
При работе этого алгоритма информация, полученная на предыдущем шаге итерации используется для построения векторов направлений поиска, а также для устранения зацикливания координатных поисков. Метод ориентирован на решение задач с квадратичными целевыми функциями и основывается на фундаментальных теоретических результатах.
Задачи с квадратичными функциями занимают важное место среди задач оптимизации по следующим причинам:

1. Квадратичная функция является простейшим типом нелинейной функции, для которой может быть сформулирована задача безусловной оптимизации. Следовательно, если с помощью того или иного метода успешно решаются задачи оптимизации с целевыми функциями общего вида, то такой метод должен оказаться эффективным при решении задач с квадратичными функциями.
2. В окрестности точки оптимума любую нелинейную функцию можно аппроксимировать квадратичной функцией, поскольку линейный член разложения в ряд Тейлора обращается в нуль. Следовательно, работа алгоритма при решении задач с квадратичными функциями позволяет получить определенное представление о сходимости алгоритма в случае, когда минимизируется функция общего вида.

Основная идея алгоритма заключается в том, что если квадратичная функция N переменных приведена к виду суммы полных квадратов, то ее оптимум может быть найден в результате реализации одномерных поисков по преобразованным координатным направлениям.

Улучшение методов переменной метрики и методов сопряженных градиентов осуществлялось весьма близкими путями. Дэвидон [95] предложил ряд модифицированных процедур, в которых не требуются точные вычисления при проведении поиска вдоль прямой. Позже Пауэлл [96], установил свойства квадратичной сходимости этих методов при отсутствии одномерных поисков. Метод переменной метрики в условиях квадратичной сходимости и отсутствия трудоемких операций одномерного поиска, может отличаться как устойчивостью, так и быстродействием при решении задач с целевыми функциями общего вида. Однако наряду с повышением степени надежности (устойчивости) алгоритмов переменной метрики, необходимость возврата к начальной итерации замедляет процесс приближения к точке оптимума, так как не позволяет использовать имеющиеся оценки производных второго порядка.
Во многих работах зарубежных авторов [97—99] широко исследованы связи между методами сопряженных градиентов и методами переменной метрики. Шенно рассматривает методы сопряженных градиентов, как методы переменной метрики в отсутствие «памяти». Большинство авторов придерживается той точки зрения, что оба класса методов обладают гораздо более существенным сходством, чем это представляется ранее. Многие варианты метода переменной метрики обладают рядом общих особенностей [100, 101], наличие которых заставляет проводить оценку трудоемкости дополнительных вычислений. Шенно и Фуа [102,103] представили многочисленные числовые результаты, которые свидетельствуют в пользу относительно простой рекуррентной формулы БФШ.
Методы переменной метрики широко используются при разработке методов решения задач условной оптимизации. В работах Хэна [104] и Пауэлла [105] исследуется вопрос эффективности этих методов при решении задач с ограничениями.
Большое количество работ посвящено применению методов переменной метрики при решении задач большой размерности. Сходство этих методов переменной метрики и квазиньютоновских дало основание для разработки обобщенного алгоритма, в основе которого лежит использование ряда рассмотренных выше методов. Таким алгоритмом является обобщенный градиентный алгоритм, подробно описанный в [106].
В обобщенном градиентном алгоритме можно использовать различные методы поиска путем определения соответствующего направления на шаге определения направления поиска S(x) в Х-м пространстве управляемых переменных.  Вычисления, необходимые далее для реализации того или иного метода, проводятся по соответствующим формулам для соответствующего метода. Тесты, включенные в обобщенный градиентный алгоритм, позволяют обнаружить любые трудности, связанные с необходимостью возврата при расчетах по методу сопряженных градиентов. Повышению эффективности обобщенного градиентного алгоритма способствует включение в него дополнительных процедур, предложенных Дэвидоном, Пауэллом и Шенно, которые позволяют избегать точных вычислений, так как на операции поиска вдоль прямой тратится значительная часть общего времени счета по программе.

Для одной и той же ЭВМ при заданных  такая аппроксимация оказывается более точной, однако при этом используется дополнительное значение функции.
В ряде случаев повышение точности аппроксимации за счет вычисления дополнительных значений функции не является оправданным.
Исследования, проведенные на строгой теоретической основе, позволили рассмотреть сходимость изложенных методов. Вместе с тем значительная часть сведений об эффективности их применения к задачам с целевыми функциями общего вида получена в результате численных экспериментов [107]. В ряде случае тестовые задачи выбираются таким образом, чтобы подчеркнуть положительные характеристики метода. Однако числовые результаты, представленные в литературе, следует использовать с известной осторожностью, так как оценки эффективности тех или иных алгоритмов, полученные только на основе анализа количества вычислений целевой функции, могут привести к неверным выводам [108].
Комбинация метод Коши и метод «деления интервала пополам» обеспечивает нахождение наиболее точного значения f(х), однако при этом требуются наибольшие затраты машинного времени. Самым эффективным по количеству вычислений значений функции оказывается метод БФШ с использованием кубичной аппроксимации. Однако для решения вопроса по преимуществу применения того или иного метода при решении конкретной задачи оптимизации, окончательный вывод можно сделать после проведения дополнительных вычислительных экспериментов.

Выводы

Только четко определив границы оптимизируемой системы, мы имеем возможность приступить к решению оптимизационной задачи. В случае оптимизации трибопараметров мы не имеем возможности определить процессы трения от параметров самого узла трения механической системы, включающей в свой состав узел трения. Таким образом, необходимо оптимизировать не параметры процессов трения, а параметры фрикционной механической системы, которую при решении оптимизационных задач нельзя разбить на подсистемы: пара трения или две пары трения (при наличии твердого тела в зоне трения), узел трения, фрикционная механическая система.

Данное положение практически исключает математическое решение оптимизационной задачи для фрикционной механической системы. Выделяя данные подсистемы, мы на порядок изменяем их выходные характеристики, что делает абсурдным попытки их оптимизации для случая их совместного функционирования.
В конечном случае задачи оптимизации фрикционных механических систем распадаются на три основных этапа:

1. построение физико-математической модели ФМС — наиболее ответственный и сложный этап;
2. получение уравнений регрессии целевой функции на базе современного аппарата математического планирования эксперимента;
3. поиск оптимума целевой и целевых функций, используя наиболее рациональный метод, дающий наиболее высокую эффективность.