2.7. Определение величины оптимального демпфирования пути
Для ответа на этот вопрос составим упрощенную математическую модель системы «экипаж—путь», которую точнее можно назвать «колесо—путь», со структурой и параметрами, выбранными на основе уже выполненного исследования полной модели «экипаж—чуть».
Упрощенная модель имеет схему, показанную на рис. 2.15, и составлена со следующими допущениями:
1. Колебания кузова не рассматриваются;

7. Демпфирование пути (как некоторое эквивалентное, учитывающее рассеивание энергии в рельсе, шпале и балласте) предстоит изменять в пределах 20:600 кНс/м.
Допущение 1-е обусловлено малой взаимной связанностью колебаний кузова и колебаний колесной пары: их собственные частоты отличаются почти на один порядок.
Допущение 2-е принято из тех соображений, что рассмотрение колебаний только тележки (без учета кузова) некорректно, а колебания тележки с учетом связей с кузовом не проявляются в резонансной форме (это пояснялось расчетом, выполненным ранее).
Допущения 3-е и 4-е позволяют увести на ∞ высокочастотные резонансы (по колебаниям шпалы и рельса) как не оказывающие существенного влияния на колебания именно колесной пары на упругом пути.
Учитывать колебания балласта следует лишь в том случае, если достаточно достоверны его свойства, в частности: масса, участвующая в колебаниях, и упруго-диссипативные характеристики его связи с основанием.
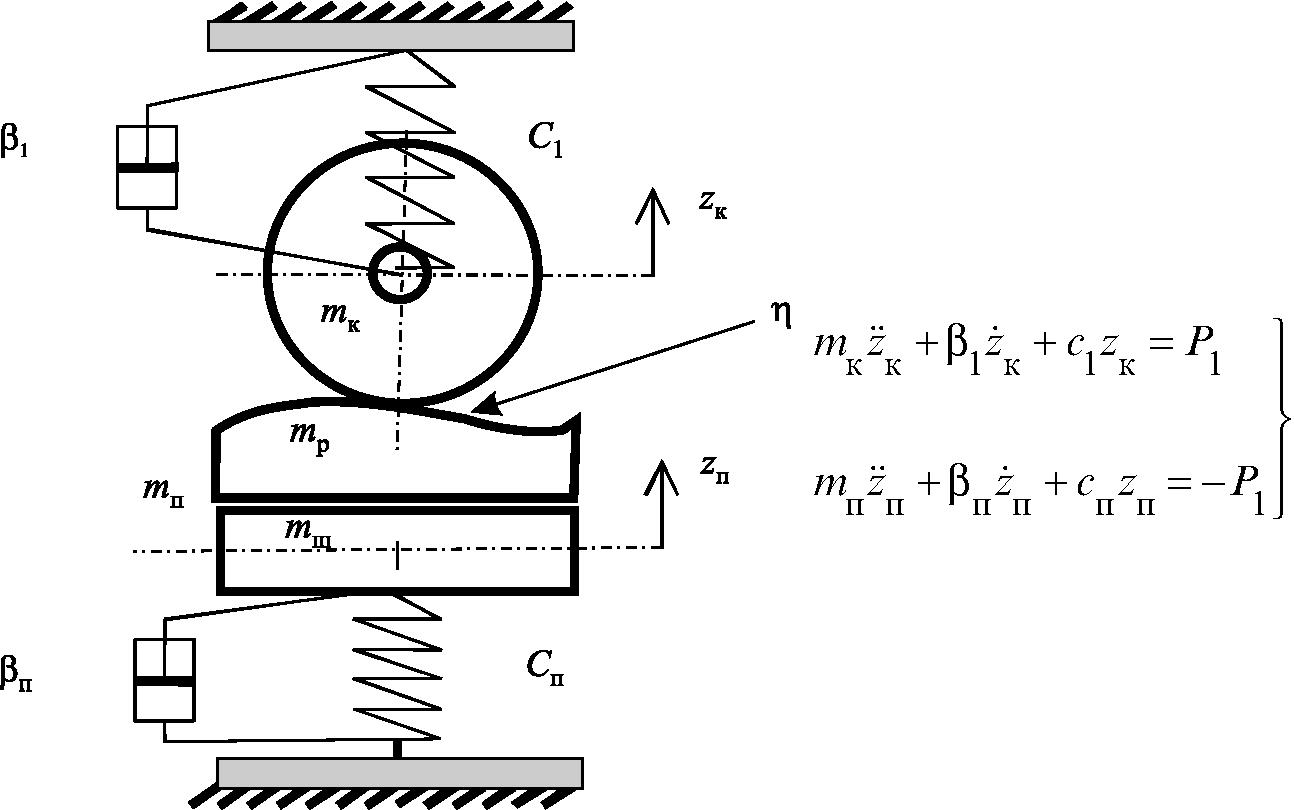
Рис. 2.15. Схема упрощенной модели
Но в этом случае придется отказаться от дискретной модели, представляющей балласт, и перейти к модели с распределенными параметрами, что существенно усложнит задачу, а, учитывая, что достоверных экспериментальных данных по инерционным и упруго-диссипативным свойствам балласта пока недостаточно (имеющиеся данные весьма противоречивы и изменяются в широких пределах, особенно в зависимости от сезона), учет колебаний балласта не внесет уточнений в рассматриваемый процесс.
Движение модели «колесо—путь» описывается дифференциальным уравнением [67]:
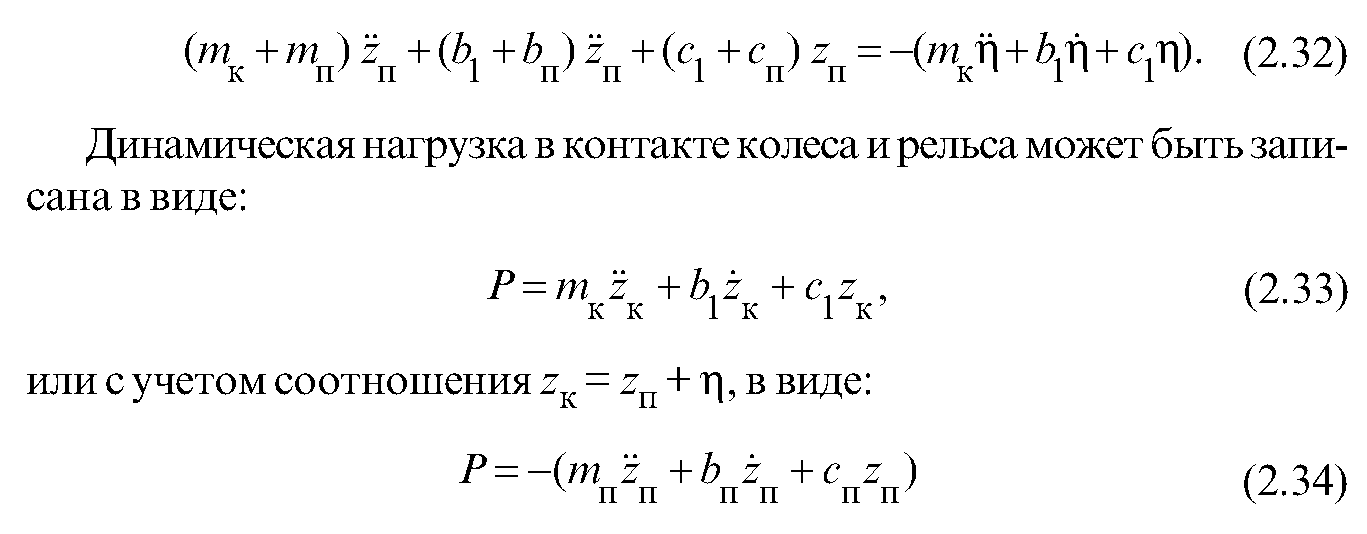
Применяя метод комплексных амплитуд, найдем Р, записав в решение уравнения (2.32) и с учетом (2.34):
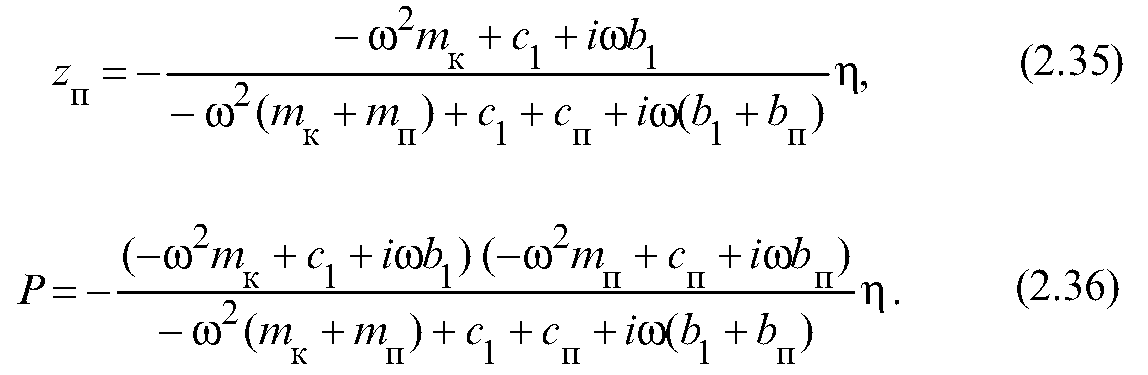
Дисперсию Ρ найдем из соотношения:
![]()
(2.37)
Для выполнения расчетов по формуле (2.37) необходимо, чтобы выражение под интегралом представляло убывающую функцию, т. е. нужно, чтобы:

где С0—некоторая постоянная.
В работе [66] приводятся данные, свидетельствующие о том, что неровность пути в области средних и высоких частот может быть представлена как «белый шум» по ускорению:

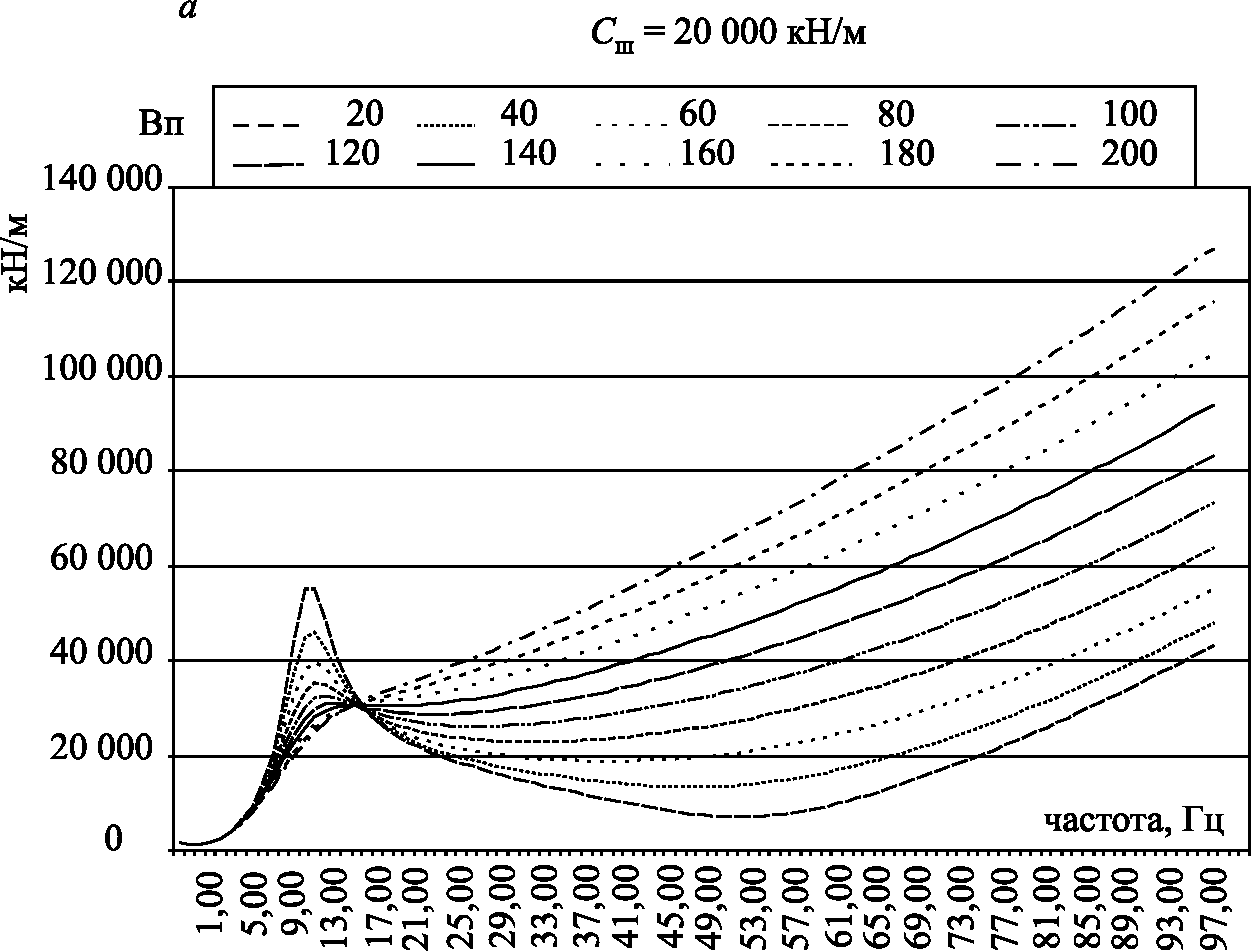
Рис. 2.16. АХЧ динамической составляющей в контакте колеса и рельса (начало)

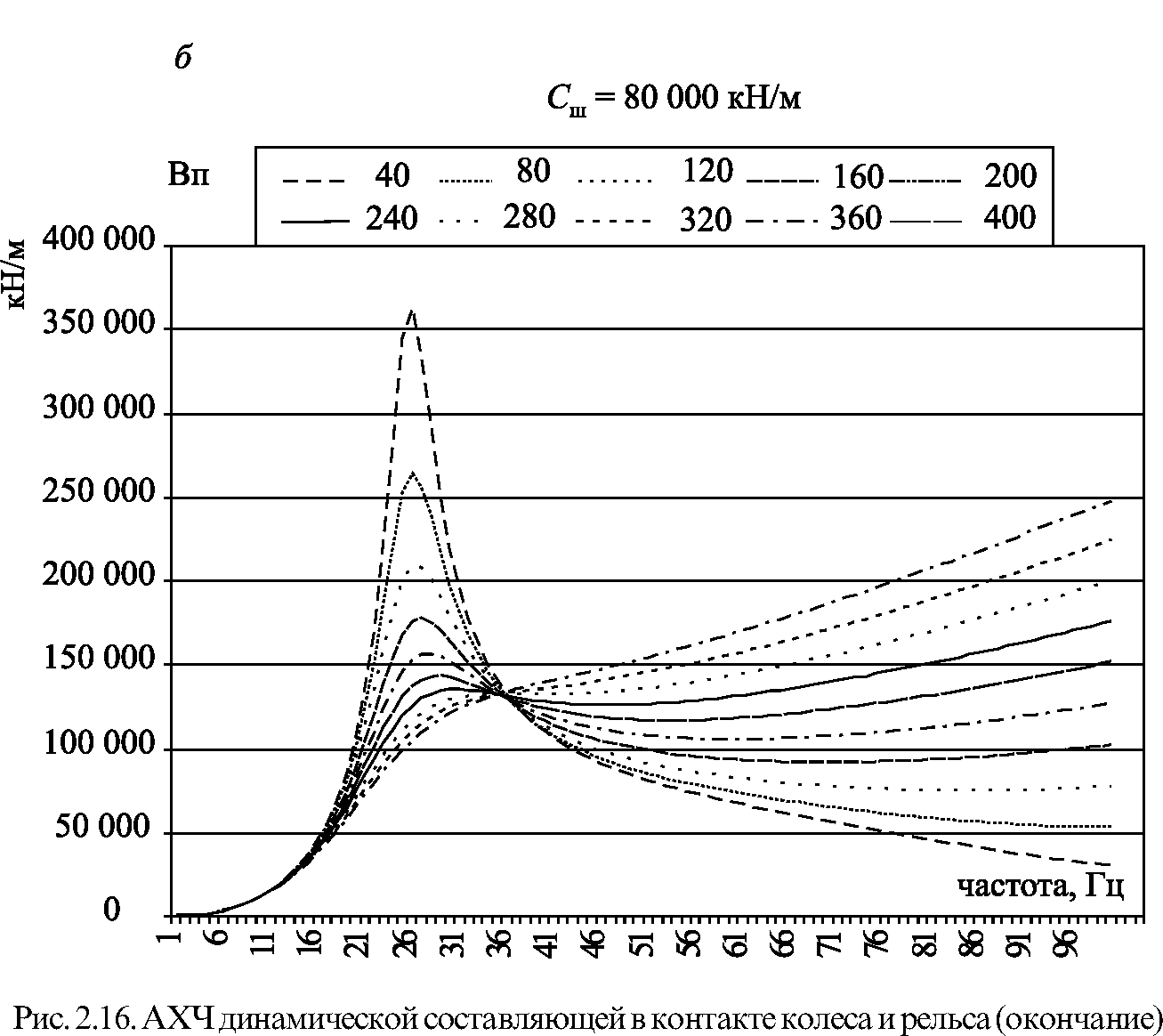
Таблица 2.2

При проектировании экипажей учитывается его динамическое воздействие на путь. Но выбор параметров ходовой части осуществляется с учетом еще целого ряда других критериев, что не всегда обеспечивает минимум динамических нагрузок в контакте колеса и рельса [70].
Для локомотива снижение уровня динамических нагрузок в контакте колеса и рельса позволяет повысить его тяговые свойства [65, 71].

Рис. 2.17. Относительная спектральная плотность динамической составляющей в контакте колеса и рельса (начало)
Поэтому применение шпалы-демпфера является одним из способов повышения тяговых качеств локомотивов и одним из перспективных шагов на пути создания динамически благоприятных условий взаимодействия пути и подвижного состава.
Выводы
- Обоснована структура математической модели.
- Разработана методика расчета статистических характеристик динамических качеств системы «экипаж—путь».
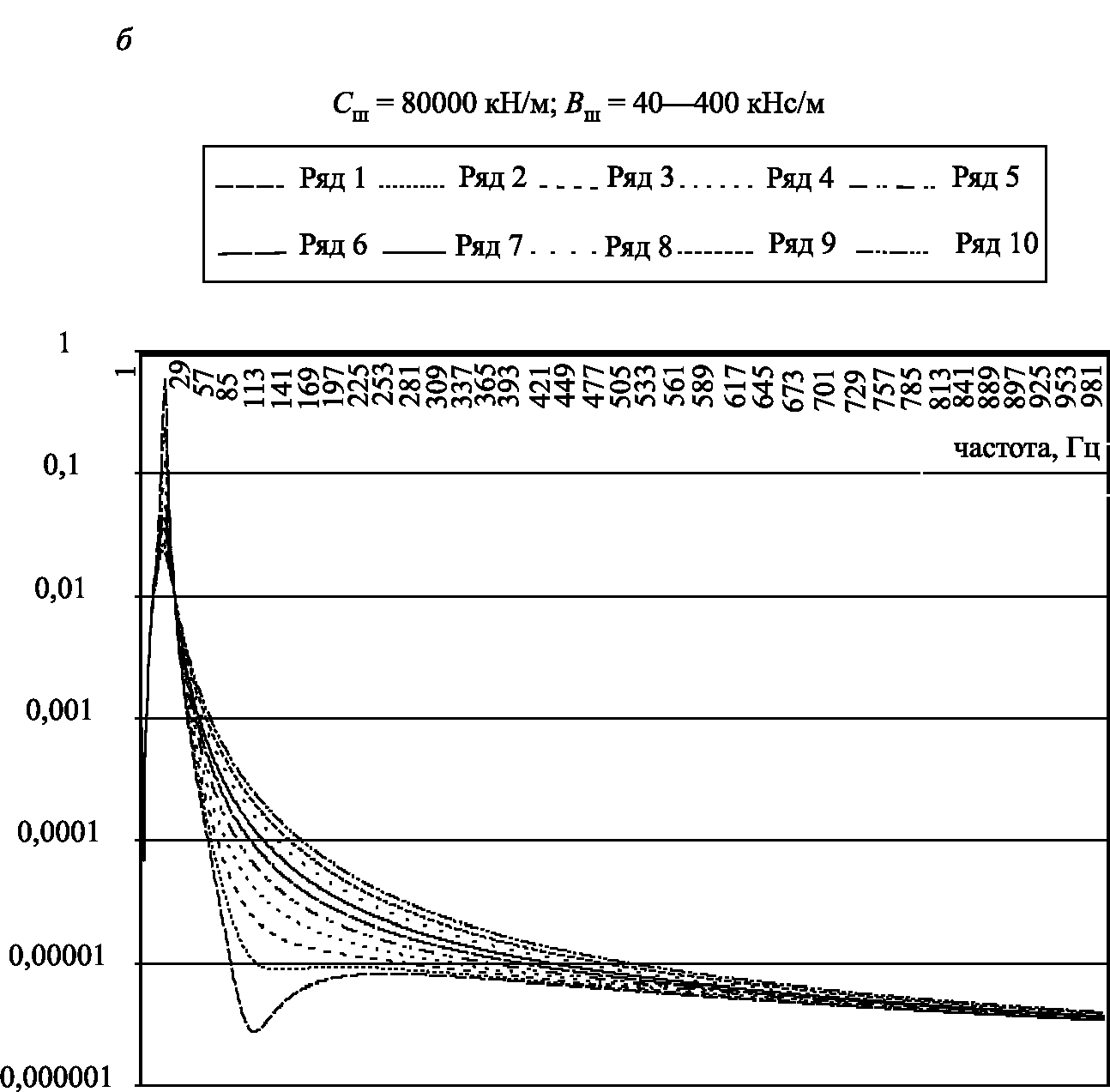
Рис. 2.17. Относительная спектральная плотность динамической составляющей в контакте колеса и рельса (окончание)
- Выполнены расчеты собственных частот и форм колебаний, построены АЧХ и спектральные плотности динамических показателей, рассчитаны среднеквадратические значения динамических показателей для диапазона скоростей движения экипажа 20—120 км/ч.
- Проведен анализ результатов расчетов и с помощью дополнительной математической модели определены оптимальные значения демпфирования пути, обеспечивающие минимум динамических нагрузок в контакте колеса и рельса.
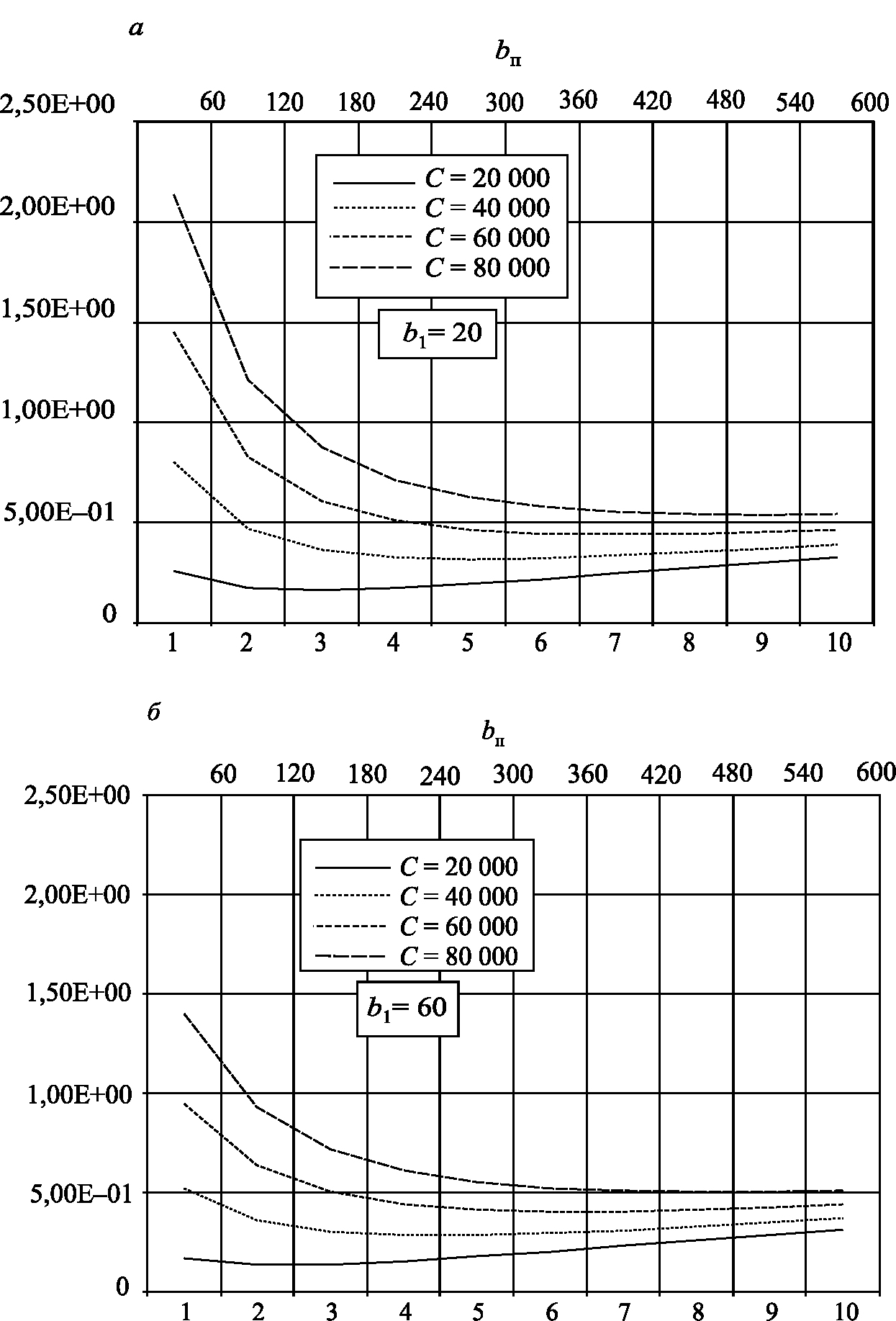
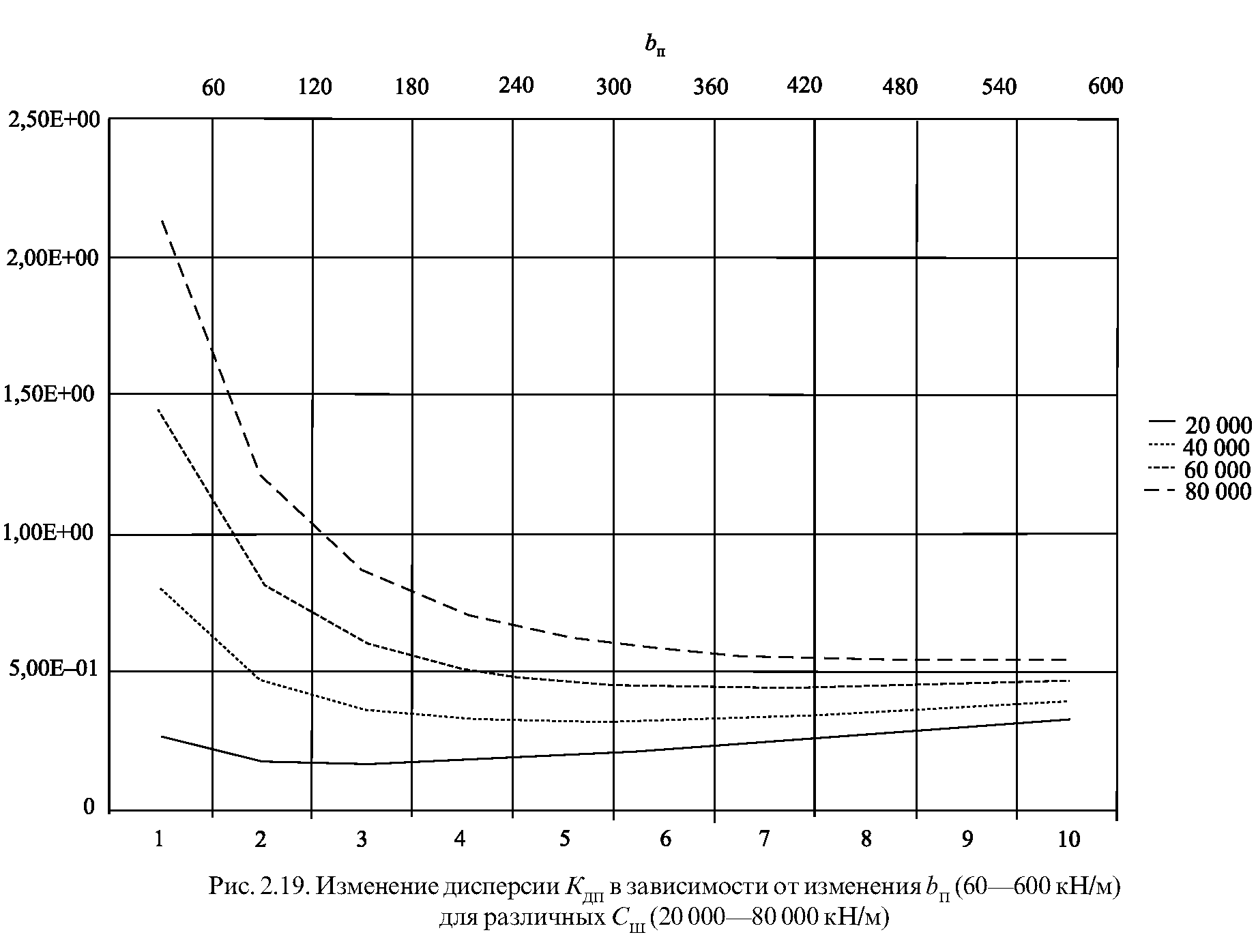
Рис. 2.18. Относительные дисперсии динамической составляющей в контакте колеса и рельса