12.2. Принципы оптимизации технологии и увеличения мощности сортировочных станций
В теории развития станционных систем и станций в целом, которые относятся к большим системам, определены фазовые и управляющие переменные, а также ограничения, накладываемые на эти переменные [15]. Это позволяет обеспечить системный подход к технологии и развитию станций, правильно формулировать и решать многовариантную задачу развития их пропускной и перерабатывающей способности, разработать прогноз их оптимального развития на перспективу на основе объективного комплексного показателя — критерия эффективности.
Для периода развития t1, tn нагрузку на систему задают в виде матриц объемов и продолжительности работы с соответствующими объемами. С другой стороны, состояния станционных систем и подсистем зависят от их внутренних характеристик: путевого развития парков, мощности каналов, занятых обработкой поездов, а также мощности выходных каналов подсистем — горки, каналов по окончанию формирования, пропускной способности выходных участков и др. Состояния подсистем определяют числом составов в подсистеме на момент времени t, т. е. величиной N (t). Фазовые переменные зависят от хода процесса в подсистемах. В самом общем виде любая из фазовых переменных представляет собой функционал Ф, определенный на траектории процесса N (t), если траектории N (t) ставится в соответствие некоторое число Ф [N (t)]. Ход процесса в подсистемах предопределяет и соответствующие значения фазовых переменных. Поэтому следует различать текущие значения этих переменных и их значения, установленные на некоторых интервалах времени достаточно большой продолжительности, например tij, в соответствии с вектором-столбцом (12.2). В связи с тем что фазовые переменные предопределены ходом процесса в подсистеме, они зависят, как и траектория процесса, от нагрузки величины поездопотока и от характеристик каналов и элементов подсистемы.
Вектор фазовых переменных для подсистемы «ВхУ—ПП—Г»

Путевое развитие подсистем в векторах (12.7)—(12.9) определяют для размеров движения Nt, соответствующих максимальному потоку (градация размеров при i=r). Пути парков создают соответствующие условия для выполнения технологических процессов. Они несут на себе функции не только фазовых, но и управляющих переменных. Например, увеличением путей в парке формирования можно повысить производительность горки и каналов формирования за счет уменьшения или полного устранения повторной переработки вагонов, вызванной недостаточным числом или длиной путей.
Если простои в подсистемах относить на один вагон, то фазовые переменные по подсистемам можно суммировать. С учетом этого получаем трехмерный вектор

где т — число подсистем.
Таким образом, развитие станции следует рассматривать в п- мерном фазовом пространстве. В данном случае число компонент вектора сведено к трем. Компоненты вектора управления составляют управляющие переменные — такие величины, которые мы можем выбирать при разработке технологии и проектировании любого этапа развития станции или узла. Применяя те или иные меры развития станции, мы увеличиваем производительность работы ее каналов — горки, каналов по окончанию формирования, ПТО, ЦТК и др.
Технологические интервалы по этим каналам — Iг, Iв, Iпто, Iцтк — это концентрированное выражение управления, а нормируемые значения интервалов при разных мерах развития станции — компоненты вектора управления. Перечень управляющих переменных для основных подсистем сортировочных станций приведен в табл. 12.2.
Если затраты на развитие каналов ПТО и ЦТК суммировать с затратами на развитие выходных каналов, то вектор управления при перспективном развитии станции можно свести к трехмерному:
![]()
Интенсификация работы выходных каналов подсистем обеспечивает рост производительности их работы. Величины этих интервалов при заданной нагрузке оказывают решающее влияние на простои, путевое развитие и эксплуатационную надежность работы станции.
Таблица 12.2
Управляющие переменные сортировочной станции

Под управлением системой в процессе ее развития следует понимать разработку, выбор и осуществление различных мер, направленных на увеличение пропускной и перерабатывающей способности станции, которые обеспечат наиболее эффективное выполнение заданного объема работы с наименьшими затратами средств.
На управляющие переменные накладываются возможные ограничения по капитальным вложениям. В этом случае в число мер развития включаются лишь такие из них, которые не требуют на каждом этапе превышения выделенных финансовых сумм на развитие станции.
Кроме того, возможны также ограничения по условию обеспечения переработки заданного поездопотока:
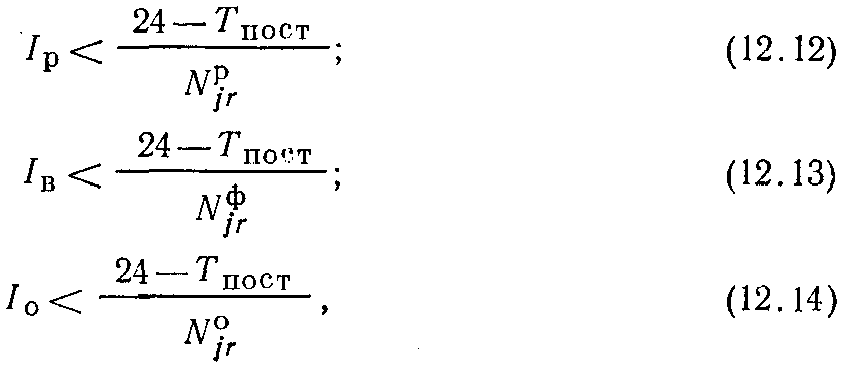

Варианты управления, не удовлетворяющие условиям (12.12)— (12.14), исключают из рассмотрения как неконкурентоспособные. Фазовые переменные в конкретных условиях развития станций и узлов могут быть ограничены также заранее установленной величиной эксплуатационной надежности работы станции, заданной величиной простоя вагонов (например, рассматривают лишь те варианты, в которых простой с переработкой не превышает 7 ч), территорией для укладки путей и другими факторами.
Существует тесная взаимосвязь между последовательностями мер (этапами) развития станции. Величины резервов перерабатывающей способности на последующем к + 1-м этапе зависят от той меры, которая была применена на к-м этапе. Вместе с резервами будет изменяться и целый ряд других показателей. Поэтому критерий эффективности, принятый для сравнения и выбора оптимальной стратегии развития станции, должен отражать также сложные функциональные взаимосвязи. Его величина на к + 1-м этапе зависит от тех мер, которые были применены на к-м этапе (шаге). При наличии нескольких последовательностей мер (более одной стратегии) оптимальные пути развития сортировочных станций выбирают методом динамического программирования. Последним, к-м, этапом (шагом) систему переводят из состояния в состояние Тк ε Ζκ (область состояний Zκ связана с тем, что на к-м этапе имеется не один, а несколько путей развития системы). При решении задачи находят так называемое условно оптимальное управление на последнем шаге, которое позволит установить локальный оптимум. Обозначим это управление Iк (Тк-1). Оно сводится к минимальному значению критерия на последнем шаге:


Совокупности векторов (12.20) соответствует искомое значение критерия эффективности планирования оптимальных этапов развития станции, а матрице векторов этапного развития станции — также и матрица оптимальных резервов перерабатывающей способности на весь плановый период:

