Кибернетические методы диагноза позволяют составить наиболее целесообразную последовательность проверок для отыскания любой неисправности с наименьшей затратой времени. Оптимальную или близкую к ней последовательность проверок можно получить, используя теорию информации. При этом нужно исходить из наличия в системе, в которой произошел отказ, какой-то начальной неопределенности. Такая неопределенность является следствием того, что наличие одного из возможных отказов в системе представляет собой случайное событие.
В процессе поиска отказа каждая проводимая проверка дает некоторую информацию, размер которой численно определяется уменьшением неопределенности (энтропии) системы. Если при проверке одного или нескольких элементов систем выяснилось, что один из них неисправен, то результат такой проверки считается положительным, в противном случае результат проверки признается отрицательным. Вероятность положительного результата Р, таким образом, может быть подсчитана заранее, если известны относительные вероятности отказов Pi каждого из элементов и то, что произошел только один отказ. Очевидно, при этом вероятность положительного результата проверки будет равна сумме вероятностей отказов тех элементов, которые не охватывались данной проверкой.
Теория информации дает возможность подсчитать убыль энтропии в результате одной проверки:
![]()
где Р — вероятность положительного результата проверки, подсчитанная указанным способом.
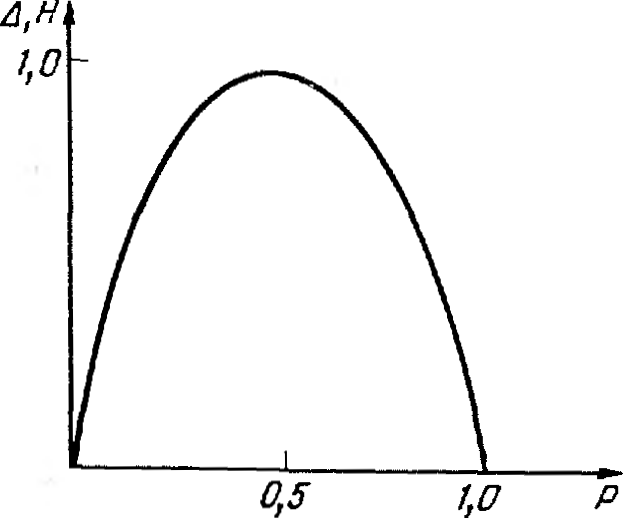
Как видно из рис. 2, максимальная убыль энтропии наблюдается в том случае, когда оба результата проверки имеют одинаковую вероятность (Р = 0,5). Естественно, что такая проверка должна выполняться в первую очередь, если не учитывать затраты времени на ее проведение. Такой метод широко применяется в практике и носит название проверки по средней точке. Однако для того чтобы любой отказ был обнаружен за минимальное время, каждая из проверок должна удовлетворять двум условиям: величина АН для проверки должна быть как можно большей; время Т, затраченное на проведение проверки, должно быть как можно меньшим. При этом каждая проверка будет характеризоваться эффективностью Θ =∆Н/Т. С учетом выполнения этих условий первой должна проводиться та проверка, которая обладает наибольшей из всех остальных эффективностью.
Рис. 2. Зависимость убыли энтропии от вероятности положительного результата проверки
Рассмотрим участок электрической цепи (рис. 3), содержащий три контакта. Предположим, что в одном из этих контактов имеется обрыв цепи, который требуется отыскать с минимальной затратой времени. Кроме того, известно, что проверки могут выполняться только измерением напряжения между определенными точками (точки а, б, в, г).
Как видно из рис. 3, в результате каждой из проверок (171 — /75) один или два контакта могут быть признаны исправными или неисправными. Если один контакт в результате первой же проверки будет признан неисправным, то на этом процесс поиска заканчивается. Если же будет установлена исправность одного контакта, то необходимо провести еще одну проверку. Следовательно, задача нахождения наиболее рационального процесса поиска заключается в выборе одного из возможных вариантов последовательности проверок.
Решим такую задачу при условии, что вероятности отказов в контактах P1= 0,1; Р2 = 0,2; Р3= 0,7, а время на проведение проверок составляет между точками а— б — 8 мин, а-в — 4 мин, б-в — 2 мин, б—г — 6 мин, в—г — 3 мин.
Результаты расчета можно свести в табл. 2, где цифрой 0 обозначены контакты, которые охватываются соответствующей проверкой, а цифрой 1 — не охватываемые проверкой.
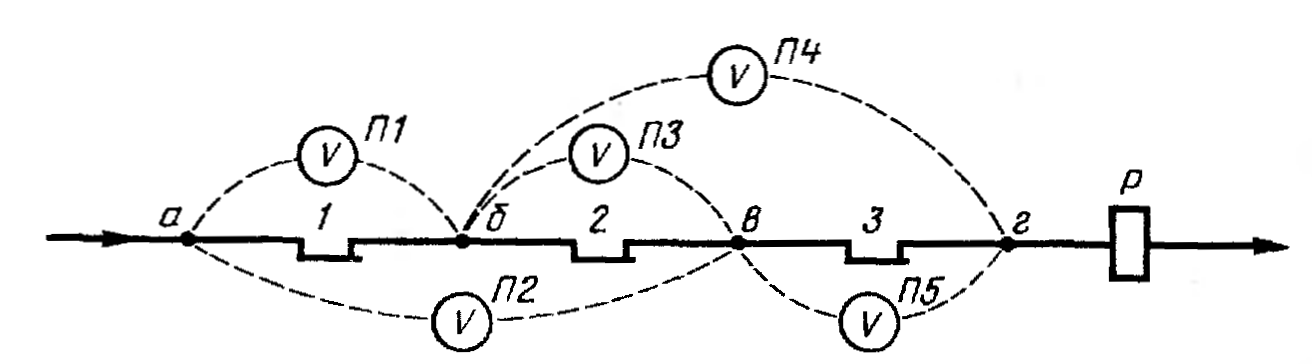
Рис. 3. Схема проверки электрической цепи
Как видно из приведенного расчета, первой надо выполнять проверку 3, как имеющую наибольшую эффективность.
Номер | Измерения между точками (напряжения) | Время | Отказы в контактах | Вероятность | Эффективность проверки θ | ||
1 | а-б | 8 | 0 | 1 | 1 | 0,1 | 0,06 |
2 | а—в | 4 | 0 | 0 | 1 | 0,3 | 0,22 |
3 | б-в | 2 | 1 | 0 | 1 | 0,2 | 0,33 |
4 | б-г | 6 | 1 | 0 | 0 | 0,9 | 0,08 |
5 | в—г | 3 | 1 | 1 | 0 | 0,7 | 0,29 |
Дальнейший расчет ведется в таком же порядке, только из контролируемой схемы исключается контакт 2 и соответственно пересчитываются значения вероятности отказов для контактов 1 и 3 (Р1 и Р3). При этом:
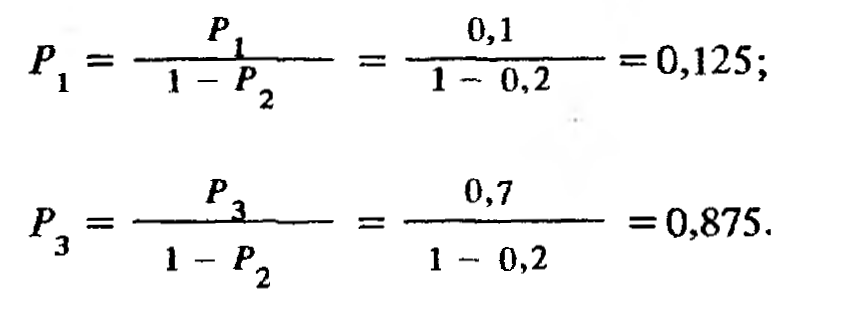
Сделав новый расчет эффективности оставшихся проверок, получим информационную диаграмму (рис. 4). Одновременно может оказаться, что при дальнейшем поиске время проведения некоторых проверок уменьшится по сравнению с тем, которое учитывалось первоначально. Так, например, если при первой проверке пульт управления был уже вскрыт с оформлением записи в журнале, то следующая проверка займет значительно меньше времени, чем она заняла бы первоначально.
В результате такого расчета может быть получена схема поиска или информационная диаграмма поиска неисправностей, которая будет указывать кратчайшие пути отыскания любой из заранее известных неисправностей.
Из разобранного примера видно, что действия по составлению оптимальной последовательности проверок (информационной диаграммы) сводятся к следующему:
определение вероятности положительного результата каждой проверки Р и затрат времени Т для каждой проверки;
вычисление значения эффективности проверки Θ по формуле эффективности и выбор проверки с наибольшим значением Θ;
определение новых состояний системы, образовавшихся в результате положительного и отрицательного доходов проверки;

Рис. 4. Информационная диаграмма поиска отказов
перерасчет относительных вероятностей отказов для элементов, оставшихся непроверенными, вероятностей положительного результата каждой оставшейся проверки с учетом результата выполненной проверки и затрат времени оставшихся проверок:
повторение процедуры до тех пор, пока последовательность не определится полностью.
