Целью этих методов является определение аналитического выражения функции колебаний надрессорного строения экипажа во времени при его движении по пути при аналитически заданных возмущающих воздействиях на экипаж. При этом должны быть известны все его механические и геометрические параметры, а также аналитически заданные функции, выражающие так называемые возмущающие воздействия на экипаж.
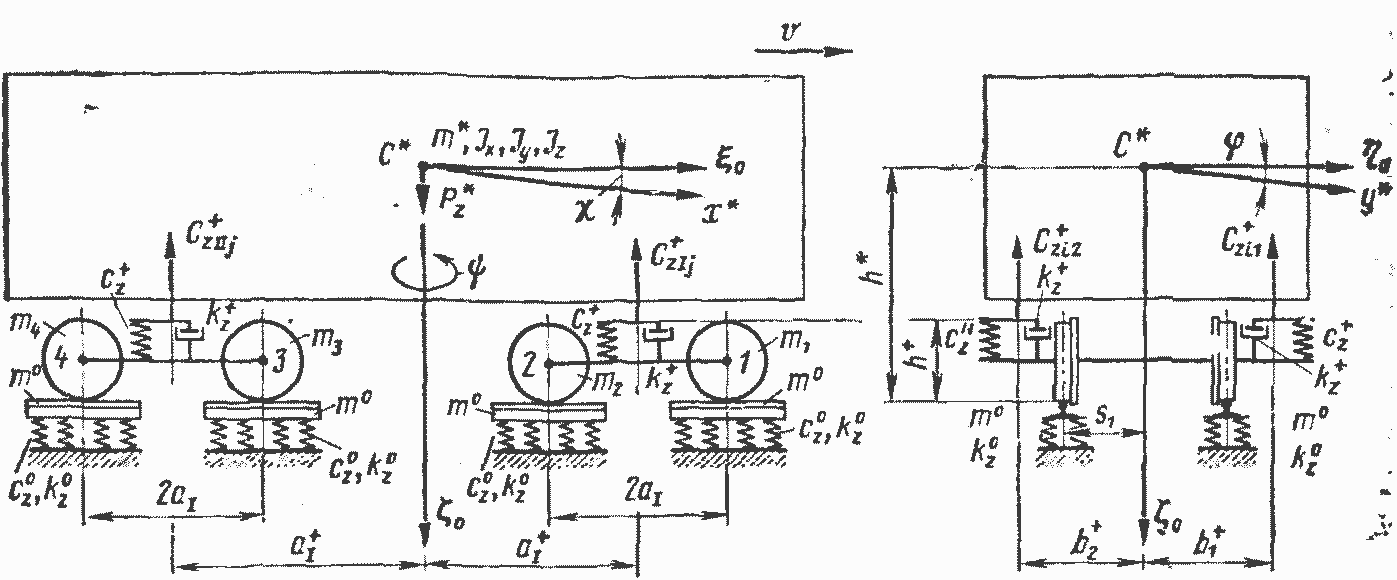
Рис. 48. Механическая модель четырехосного экипажа с одноступенчатым рессорным подвешиванием
К числу таких возмущающих воздействий относят неровности в профиле и плане по каждому из рельсов железнодорожного пути, неровности во взаимном расположении этих рельсов, неровности на поверхностях катания колес, эксцентричную или непараллельную посадку колес на осях, а для некоторых видов экипажей и неуравновешенные инерционные силы, возникающие при работе установленных на таких экипажах машин и механизмов.
Для определения аналитического выражения функций колебаний надрессорного строения во времени необходимо иметь математический оператор, используя который по отношению к функциям, описывающим возмущающие воздействия на экипаж, можно получить искомые функции его колебаний. Построение таких операторов основано на составлении систем линейных или нелинейных дифференциальных или интегродифференциальных уравнений, описывающих железнодорожный экипаж и путь как некоторую механическую колебательную систему.
Покажем один из простейших методов построения такого оператора на примере решения задачи о колебаниях элементов экипажа на одинарном рессорном подвешивании. Этот метод может быть легко распространен и на другие типы экипажей.
Расчетная схема для такого экипажа показана на рис. 48; при этом принимаются обозначения, описанные в приложении 1. В этой модели кузов и рамы тележек считают жесткими, а верхнее строение пути — упругим и обладающим приведенной массой.
В такой системе кузов на рессорном подвешивании может совершать колебания подпрыгивания, галопирования, боковой качки, бокового относа и виляния, т. е. имеет пять степеней свободы. Кроме того, каждая из тележек совместно с приведенной массой пути может совершать те же пять видов колебаний. Таким образом, кузов и две тележки в сумме имеют 15 степеней свободы2.
1 Впервые этот термин и понятие введено в теорию взаимодействия пути и подвижного состава в работе [19].
2 Здесь не рассматривается возможность продольных колебаний экипажа (подергивания) при его движении в поезде.
Если при стоянке экипажа произвольно направленным силовым импульсом вывести кузов из состояния равновесия, то все элементы экипажа начнут совершать затухающие колебания с собственными частотами, значения которых зависят от значений и размещения масс, входящих в экипаж, моментов инерции, значений жесткостей соответствующих связей (в подвижном составе и пути) и характеристик гасителей колебаний. Знание собственных частот колебаний экипажа необходимо во всех исследованиях взаимодействия пути и подвижного состава.
На рис. 52, а в качестве примера показаны графики модуля АЧХ для четырехосных грузовых вагонов на тележках типа ЦНИИ-Х3 (с жесткостью рессорного подвешивания тележки 4МН-М-1); на рис. 52, б показаны графики модуля АЧХ при различных параметрах демпфирования.
В работах [97, 99] получены ПФ, ЧХ и АЧХ для ряда других экипажей и, в частности, для грузового вагона с центральным подвешиванием тележек с шестью, девятью и одиннадцатью степенями свободы и пассажирского вагона с двойным подвешиванием с шестью и десятью степенями свободы, а также с учетом упругости пути. Полученные для указанных выше случаев ПФ и ЧХ представляют собой весьма громоздкие алгебраические формулы, требующие большого труда на их вычисления. Для таких вычислений целесообразно использовать ЭЦВМ.

Для решения многих задач взаимодействия пути и подвижного состава и, в частности, задач о колебаниях надрессорного строения целесообразно использование и электронных аналоговых вычислительных машин (ЭАВМ).
Решение задач на ЭАВМ представляет собой процесс математического моделирования физической модели (объекта). При этом автоматически непрерывно во времени осуществляются математические операции в уравнениях, описывающих реальные процессы в физической модели (объекте). Эти математические операции осуществляются с помощью электронных блоков (усилителей постоянного тока).
Различные разновидности таких блоков (решающих элементов) способны осуществлять алгебраическое суммирование, умножение на постоянный коэффициент, перемену знака (инвертирование), интегрирование, дифференцирование, нелинейные функциональные преобразования, моделирование переменного от какого- то заданного аргумента и другие математические операции. В число этих блоков могут входить и такие, которые воспроизводят какие-либо детерминированные заранее задаваемые функции или детерминированные реализации случайных процессов; они обычно используются для задания возмущающих функций в механических системах (функции, обычно стоящие в правых частях уравнений).
Таким образом, соединив по заранее составленной блок-схеме решающие элементы, можно создать автоматическое электронное устройство, непрерывно осуществляющее процессы, идентичные какому-либо заранее составленному уравнению, описывающему процессы в реальном физическом объекте. Переменными величинами в таких устройствах будут электрические параметры; чаще всего для этого используются величины электрических напряжений, называемые в этом случае машинными переменными.
Машинные переменные выбираются обычно пропорциональными действительным переменным. Соотношения между математическими переменными в уравнениях динамики и машинными переменными устанавливаются с помощью масштабных коэффициентов. Действительные уравнения с помощью масштабных коэффициентов преобразуют в машинные уравнения.
На основе записей машинных уравнений строятся блок-схемы, на которых показываются все решающие элементы (с указанием их параметров), участвующие в решении данной задачи, их передаточные функции, соединение элементов между собой, в соответствии с машинными уравнениями, и характерные точки схемы, где реализуются и могут быть зарегистрированы те или иные машинные переменные. Кроме того, на них наносятся блоки, задающие возмущающие детерминированные функции.
На основе таких блок-схем из решающих блоков монтируется электрическая модель задачи на ЭАВМ, осуществляются ее испытания с помощью простейших тестовых задач и решается поставленная задача в машинных переменных. При этом регистрируются выходные машинные переменные, получаемые в заданных точках схемы ЭАВМ, с помощью осциллографов или других регистрирующих устройств. Зная масштабные коэффициенты по осциллограммам можно легко получить искомые функции решения уравнений, в частности дифференциальных уравнений, описывающих динамические процессы в подвижном составе.
Большим преимуществом решения задач взаимодействия пути и подвижного состава на ЭАВМ, в сравнении с другими методами, является возможность введения в решения дифференциальных уравнений в виде произвольных реализаций случайных функций (неровностей на пути и колесах), введения существенно нелинейных функций и коэффициентов в этих уравнениях, получение результатов в наглядной форме. В то же время конечная точность таких решений ниже, чем у цифровых машин, и относительная ошибка в получаемых результатах может достигать 5—10%.
Теория и практика использования ЭАВМ для решения математических задач и, в частности, задач о колебаниях подвижного состава с заданными характеристиками при известных функциях возмущающих воздействий представляют собой специальную дисциплину и освещены, например, в работе [100].
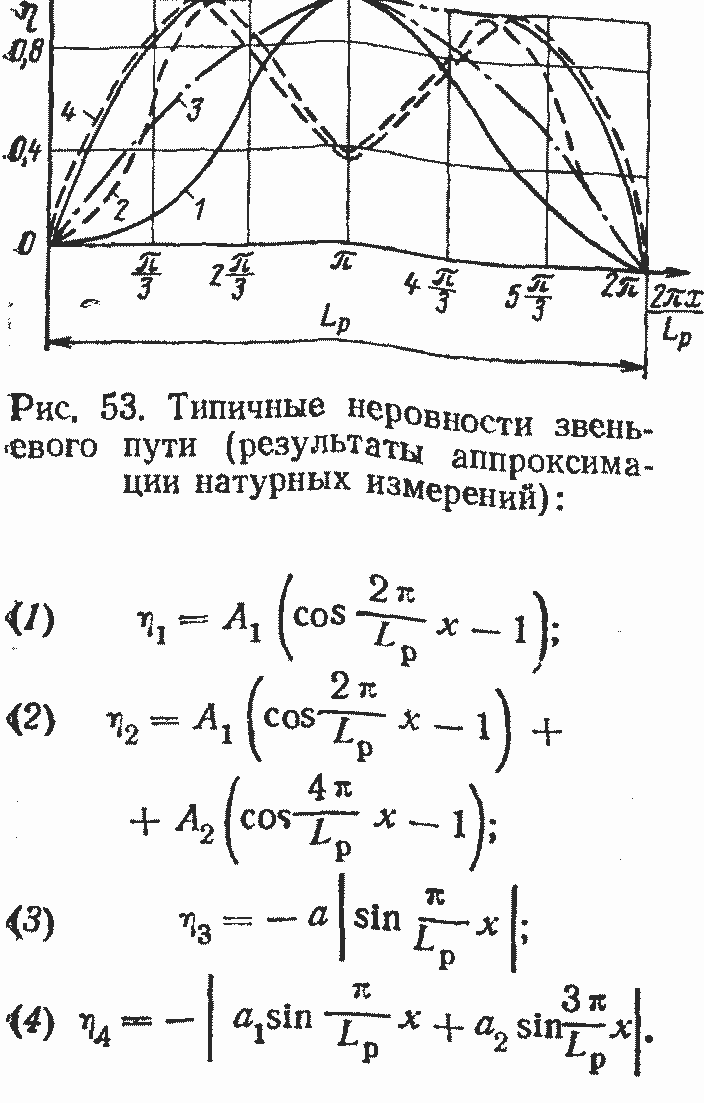
Одним из элементов, определяющих точность решения задачи о колебаниях надрессорного строения экипажей, является правильный выбор или назначение функций, описывающих неровности в пути и на колесах подвижного состава.
Наибольшие возмущающие воздействия на подвижной состав возникают на звеньевом пути, для которого характерной особенностью является наличие периодически следующих по ходу экипажа стыковых неровностей. Осредненная форма этих неровностей и некоторые графики неровностей с предложенными ВНИИЖТ МПС формулами, аппроксимирующими эти неровности, приведены на рис. 53.
Обычно в практических расчетах и исследованиях вертикальных колебаний надрессорного строения экипажей в функции f(t)не учитывают упругие деформации пути под влиянием переменных динамических нагрузок, передаваемых колесами рельсам. При этом могут быть получены лишь приближенные решения задач о колебаниях надрессорного строения и тележек, поскольку форма и размеры неровностей пути с учетом переменных по ходу колеса прогибов рельса несколько отличаются от чисто геометрических неровностей пути. Как показывает практика расчетов вертикальных колебаний надрессорного строения, неучет упругости пути не приводит к ошибкам, превышающим 1—3%.
Вместе с тем в этих расчетах должны учитываться полные размеры геометрических неровностей пути под катящимся колесом при постоянно действующей на это колесо нагрузке (размеры так называемых силовых неровностей); силовая неровность состоит из геометрических неровностей поверхности катания рельсов, дополнительных прогибов рельсов, образующихся за счет сжатия случайных зазоров, имеющихся между элементами верхнего строения пути (рельсами и скреплениями, скреплениями и шпалами, шпалами и балластом) в незагруженном состоянии пути, и деформаций из-за неравножесткости пути по его протяжению. В расчетах вертикальных колебаний тележек неучет упругих деформаций пути приводит к более заметным погрешностям. Расчеты вертикальных колебаний колесных пар (неподрессоренных масс) без учета упругих деформаций пути вообще недопустимы, поскольку могут привести к грубым ошибкам.
Расчет вертикальных колебаний надрессорного строения экипажа, вызванных неровностями на колесах или их эксцентричной насадкой на оси, принципиально ничем не отличается от описанного выше. Отличие решения заключается лишь в том, что неровности на различных колесах одного и того же экипажа различны и поэтому число «входов» в эту систему, а следовательно, и число членов в правой части уравнений (3.37) будет равно числу колес, имеющих те или иные неровности на поверхности катания. Дальнейший ход решения задач о вертикальных колебаниях надрессорного строения совпадает с приведенным выше.
Возмущающие силы, действующие на надрессорное строение локомотивов, могут возникать также в виде неуравновешенных сил инерции двигателей или вспомогательных агрегатов. Однако эти силы или малы, или по частотам своим весьма далеки от собственных частот колебаний экипажа. Так, даже у самых неблагоприятных с этой точки зрения локомотивов — тепловозов возмущающая сила, вызываемая, например, неуравновешенностью коленчатого вала дизеля, имеет частоту примерно в 30 раз выше собственной частоты вертикальных колебаний надрессорного строения [101], т. е. эта сила не может дать сколько-нибудь заметных колебаний надрессорного строения. Несколько большие значения имеют неуравновешенные силы инерции в двухтактных дизелях (например, 2Д100), где могут возникнуть возмущающие силы инерции с более низкими частотами. Однако, как показывает расчет, и в этом случае возмущающая нагрузка на тележку не превышает 0,25 кН и, очевидно, не сможет раскачать кузов.
Значительно большие неуравновешенные силы могут возникнуть вследствие некоторого различия в значениях массы разных элементов шатунно-поршневых групп дизеля (на наших заводах при сборке и ремонтах допускается разность до 0,4—0,5 кг). Эти силы могут достигать 0,8—1,0 кН и имеют частоту, равную числу оборотов двигателя.
Несмотря на то что указанные выше силы невелики, при проектировании локомотивов следует учитывать их в расчетах вибраций или колебаний кузова. Для этого следует учесть еще один «вход» в динамическую систему экипажа, прилагая в точке возникновения колебаний двигателя в кузове гармоническую составляющую вида
![]() (3.54)
(3.54)
где Аk — амплитудное значение возмущающей силы; k — номер гармоники колебаний; — угловая частота вала двигателя.
Если составляющая возмущающих колебаний находится в центре тяжести кузова (в большинстве случаев в приближенных расчетах это может быть допущено), то достаточно силу Q ввести в правую часть уравнения подпрыгивания [в системе уравнений (3.37)].
Причинами колебаний экипажа могут быть также некоторые нагрузки, близкие по характеру к импульсному силовому воздействию на экипаж. В частности, такими нагрузками являются инерционные нагрузки, возникающие при резком торможении, трогании с места экипажа, а также при входе его в кривые, переводные кривые стрелочных переводов и выходе из этих кривых.
Как указывалось, такое же импульсное силовое воздействие экипаж испытывает при входе и выходе из кривых, после чего возникают собственные колебания надрессорного строения. Следовательно, задача опять сводится к нахождению начальных амплитуд колебаний А и Αφ. Собственные колебания и в этом случае могут быть описаны приведенными выше формулами.
Учитывая, что обычно экипажи представляют собой линейно-деформируемые динамические системы, т. е. в решении задач о их колебаниях применим принцип суперпозиции (наложения колебаний), возникающие от импульсных нагрузок колебания должны накладываться на колебания, вызванные другими причинами.
Для систем, где сопротивление гасителей колебаний пропорционально их перемещениям, как показано в работе [103], эквивалентный коэффициент:
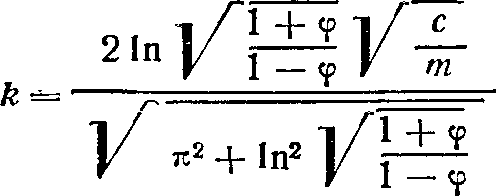
Из изложенного видны существенные условности в детерминистическом решении задач о колебаниях надрессорного строения при геометрически заданных формах неровностей пути и колес. Однако этот метод обладает и существенными положительными качествами; он позволяет строить и исследовать АЧХ экипажей при различных их параметрах и устанавливать пути снижения амплитуд этих колебаний. Это хорошо видно на примерах АЧХ, приведенных на рис. 52, б, где показано влияние выбора характеристик демпфирования системы на максимумы и общее течение АЧХ. Особенно мощным продолжением этого метода является его соединение с теорией случайных функций.
