ЭЛЕКТРОМАГНИТНЫЕ ПРОЦЕССЫ В СИЛОВЫХ ЦЕПЯХ ЭПС С УЧЕТОМ СВОЙСТВ ИСТОЧНИКА ПИТАНИЯ
Особенности электромагнитных процессов в силовых цепях
Анализ процессов в асинхронном двигателе и преобразователях частоты обычно выполняют в предположении независимости входных токов и напряжений от режима и условий работы ЭПС. В реальных системах параметры источника питания, емкость конденсатора фильтра и индуктивность сглаживающего реактора имеют конечные значения, а мощность нагрузки соизмерима с мощностью источника питания. Энергию, поступающую от контактной сети к тяговым двигателям, подвергают многократным преобразованиям, используя входные и выходные преобразователи. Поскольку входные преобразователи выполняются на полупроводниковых приборах, имеющих нелинейные характеристики, при таком преобразовании наряду с основными составляющими токи и напряжения содержат значительные дополнительные переменные составляющие.
В свою очередь выходные преобразователи, обладая частотно-избирательными свойствами, могут усиливать эти переменные составляющие, значения которых достигают (а иногда и превышают) значения основной составляющей.
На рис. 8.1 для примера показан характер изменения тока и напряжения инвертора, а также выпрямленного напряжения ud и тока выпрямителя id при питании асинхронного двигателя от инвертора напряжения с частотой = 17,5 Гц. Наряду с переменными составляющими, обусловленными выпрямленным напряжением, появилась дополнительная гармоника с частотой 5 Гц и амплитудой, равной основной составляющей. Как будет показано дальше, эта гармоника в токах и напряжении возникает в результате взаимодействия гармоники напряжения ud с частотой 100 Гц и гармоники тока инвертора с частотой 105 Гц.
Уже одного этого примера достаточно, чтобы показать, что неучет конечных параметров фильтра, свойств источника питания и входного преобразователя, взаимного влияния элементов тягового привода приводит к ошибкам при анализе электромагнитных процессов в силовых цепях ЭПС с асинхронным тяговым двигателем. Поэтому тяговый привод с асинхронными двигателями следует рассматривать как сложную систему, содержащую ограниченное множество элементов, объединенных определенными связями, используя для его анализа системный подход [33]. При этом в целой системе можно выделить подсистемы, представляющие некоторую часть элементов системы, выполняющих определенные функционально завершенные преобразования. В зависимости от степени детализации функциональных преобразований, выполняемых подсистемами, любая сложная система может быть представлена различным числом подсистем.
Так, в одном из вариантов тяговая система может содержать подсистемы электропитания, локомотив и поезд. В свою очередь каждая подсистема или элемент системы может рассматриваться как система. Рассматривая подсистему локомотив с асинхронным тяговым двигателем применительно к решаемой задаче как систему, в ней можно выделить подсистемы, соответствующие электрической, механической и управляющей частям [34], каждая из которых выполняет функционально завершенные преобразования.
В подсистеме Электрическая часть осуществляется преобразование электрической энергии, поступающей от системы электропитания, в механическую энергию на валу асинхронного тягового двигателя.
Подсистема Механическая часть преобразует момент на валу тягового двигателя в силу тяги или торможения, действующую на поезд и реализуемые вследствие наличия сцепления движущих колес с рельсами.
Подсистема Управляющая часть в соответствии с заданным алгоритмом осуществляет преобразование выходных координат, характеризующих состояние системы, в управляющие воздействия на электрическую часть системы.
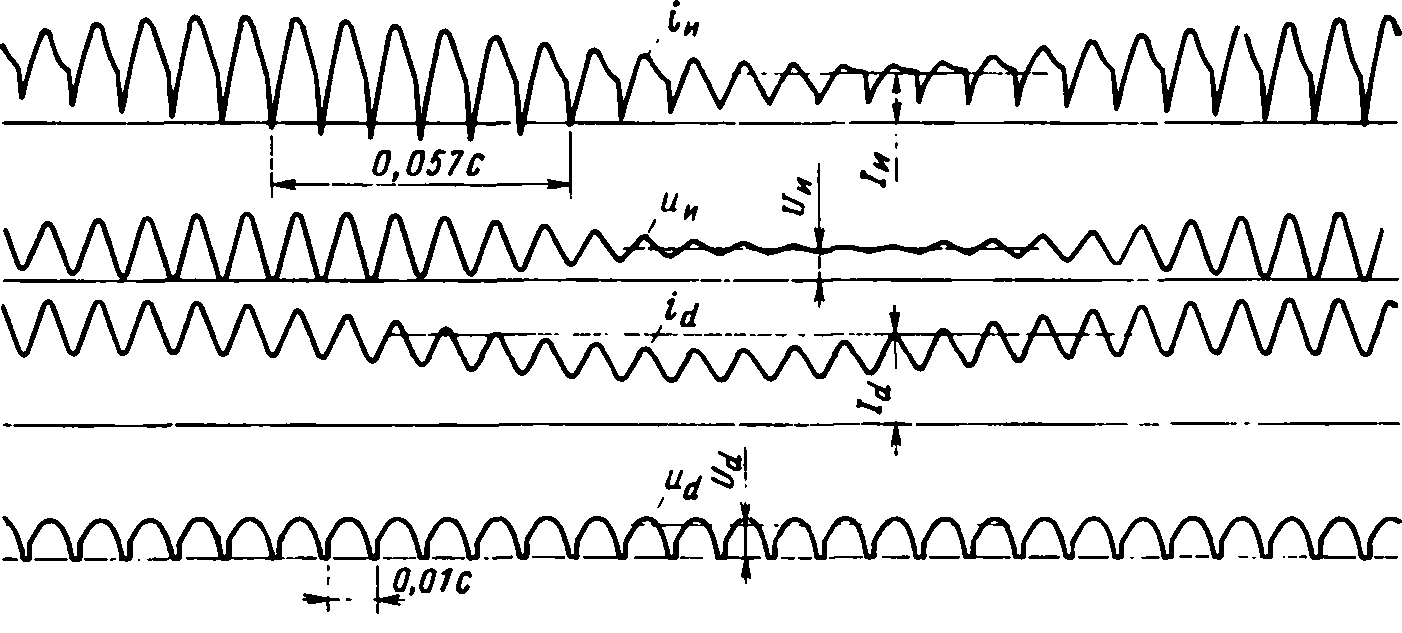
Рис. 8.1. Кривые токов и напряжений элементов системы асинхронного тягового привода при f1= 17,5 Гц

Рис. 8.2. Функциональная схема системы тягового привода с асинхронными двигателями
Поскольку каждая система или подсистема окружена внешней средой, то она взаимодействует с ней посредством входных воздействий со стороны внешней среды на систему и выходных воздействий со стороны системы на внешнюю среду. При этом в качестве внешней среды по отношению к конкретной подсистеме могут выступать другие подсистемы, образующие целую систему. Каждая система может быть формализована и представлена некоторой математической моделью ее функционирования. При этом различают детерминированные математические модели, которые могут быть статическими и динамическими [35, 37].
В обобщенную функциональную схему системы асинхронного тягового привода (рис. 8.2) входят подсистемы, соответствующие электрической, механической и управляющей частям. В качестве входных и выходных воздействий для каждой подсистемы следует рассматривать следующие.
Электрическая часть: входные воздействия — напряжение контактной сети, угловая скорость вращения ротора АТД ω, сигналы управления; выходные — ток в контактной сети, вращающий момент М на валу асинхронного тягового двигателя, наблюдаемые переменные Z1 .... Zm.
Механическая часть: входные воздействия — момент двигателя и скорость движения υ; выходные — угловая скорость вращения ω, сила тяги F н наблюдаемые переменные Zm+1, ..., Zn.
Управляющая часть: входные воздействия — наблюдаемые переменные Zj Z; выходные — сигналы управления μ.
Все подсистемы взаимодействуют друг с другом, причем выходные воздействия одной подсистемы являются входными для другой. Поэтому достоверные результаты анализа процессов в системе асинхронного тягового привода во всех режимах могут быть получены при моделировании всех указанных подсистем [38]. Вместе с тем подсистемы могут рассматриваться как самостоятельные, если выполняется следующее условие: изменение выходных координат подсистемы не приводит к изменению входных. Применительно к подсистеме Электрическая часть выполнить это условие возможно при независимости напряжения в контактной сети от тока и постоянства частоты вращения ротора асинхронных тяговых двигателей. Для этого необходимо, во-первых, параметры контактной сети учесть в параметрах элементов электрической части; во-вторых, рассматривать режимы, при которых момент на колесной паре не превышает момента сил сцепления, и, в-третьих, рассматривать установившиеся режимы для подсистемы Управляющая часть.
С учетом сказанного подсистему Электрическая часть можно рассматривать как самостоятельную. В нее входят элементы: входной фильтр Ф1, входной преобразователь П1, промежуточный фильтр Ф2, выходной преобразователь П2 и асинхронный тяговый двигатель АТД. В некоторых случаях в зависимости от структурного построения преобразователя для питания асинхронного тягового двигателя отдельные элементы в системе могут отсутствовать, например, при питании ЭПС от контактной сети постоянного тока и использовании АИН с внутренним регулированием.
Функциональную схему подсистемы Электрическая часть следует использовать при анализе электромагнитных процессов в силовых цепях ЭПС в установившихся по отношению к внешним воздействиям режимах. Выделение же из указанной подсистемы отдельных элементов возможно только для изучения каких-либо определенных их свойств.
Все элементы подсистемы Электрическая часть взаимодействуют друг с другом. В качестве входных и выходных воздействий могут выступать токи или напряжения. Сигналы управления, поступающие па элементы подсистемы Электрическая часть, несут информацию о требуемых параметрах напряжения или тока на выходах преобразователей.
Для анализа электрической части системы асинхронного тягового привода необходимо составить математические модели каждого элемента, объединив которые, получим математическую модель всей подсистемы.
Математическое описание процессов в каждом элементе подсистемы не представляет особых затруднений. При этом математические модели «непрерывных» элементов подсистемы, таких, как фильтры, асинхронные тяговые двигатели, могут быть представлены системой дифференциальных уравнений. Для преобразователей, при условии замены тиристоров и диодов идеальными ключами, следует использовать алгебраические уравнения, устанавливающие связь между входными и выходными параметрами. Поскольку в процессе работы преобразователей состояние тиристоров и диодов изменяется в соответствии с алгоритмом их переключения, то уравнения, описывающие процессы в преобразователях, являются кусочно-непрерывными. Это приводит к тому, что каждому интервалу фиксированного состояния полупроводниковых приборов соответствуют свои системы уравнений, отличающиеся либо числом уравнений, либо коэффициентами.
Для исследования таких систем применяется кусочно-линейный метод, основанный на численном интегрировании дифференциальных уравнений.
Являясь наиболее точным, этот метод имеет ряд недостатков: сложность, громоздкость при анализе больших систем, недостаточная наглядность в выявлении общих закономерностей, большие затраты времени при исследовании установившихся процессов и получении интегральных оценок.
Создание же точных аналитических методов для анализа процессов в электрических цепях, содержащих полупроводниковые преобразователи, в общем случае является чрезвычайно трудным и практически не представляется возможным. Однако если рассматривать процессы при неизменных сигналах управления преобразователями, то задача существенно упрощается и может быть сведена к исследованию электрических цепей с переменными, периодически изменяющимися параметрами [38, 391. В этом случае расчет электромагнитных процессов в силовых цепях может быть выполнен спектральным методом, основанным на использовании преобразования Фурье [40].
Сущность спектрального метода анализа процессов в электрических цепях, содержащих полупроводниковые преобразователи, заключается в следующем:
для «непрерывных» элементов подсистемы, входных и выходных по отношению к преобразователю цепей, составляют уравнения электрического равновесия, выражая входящие в них переменные через входные и выходные токи и напряжения преобразователя;
на основании алгоритма работы преобразователя, а также баланса мощности со стороны входа и выхода преобразователя составляют уравнения связи между входными и выходными токами и напряжениями, для чего используют переключающие или коммутационные функции. Так как последние являются периодическими кусочно-непрерывными функциями времени, то их представляют при помощи рядов Фурье;
решая полученную таким образом систему уравнений одним из известных методов, находят выражения для искомых переменных, которые используют для анализа переходных и установившихся режимом работы схемы [38—41].
Так как для ЭПС наиболее характерным является установившийся режим работы, то в дальнейшем анализ процессов в силовых цепях выполнен применительно к этому режиму.
В качестве «непрерывных» элементов в зависимости от структуры преобразователя на ЭПС могут применяться индуктивные, емкостные, индуктивно-емкостные фильтры, а также трансформаторы (рис. 8.3, а—г) и асинхронные тяговые двигатели. Независимо от сложности схемы «непрерывных» элементов уравнения электрического равновесия для них должны быть составлены таким образом, чтобы в них содержались входные и выходные токи и напряжения преобразователей, иными словами, «непрерывные элементы» необходимо рассматривать как пассивные четырехполюсники.
