2. КРАТКАЯ ХАРАКТЕРИСТИКА МАТЕМАТИЧЕСКИХ МЕТОДОВ, ПРИМЕНЯЕМЫХ В ТЕОРИИ НАДЕЖНОСТИ.
Теория надежности — это наука, изучающая закономерности распределения отказов технических устройств, причины и модели их возникновения. Выводы и положения теории надежности используются при проектировании, изготовлении, приемке, эксплуатации и хранении объектов, для расчета качественных характеристик изделий, обеспечения технико-экономической эффективности и прогнозирования их состояния в заданных условиях эксплуатации. Такой комплексный характер науки о надежности позволяет заключить, что она является методологической основой, определяющей целевую направленность инженерных и специальных технических дисциплин при решении задачи обеспечения высокого уровня безотказности тягового подвижного состава.
Чтобы наука о надежности отвечала поставленным перед нею задачам и была способной давать точные заключения, обоснования и выводы, она должна иметь соответствующий математический аппарат, который объединяет в одну систему модели и методы, с помощью которых решают проблемы оценки, прогнозирования, оптимизации различных показателей надежности.
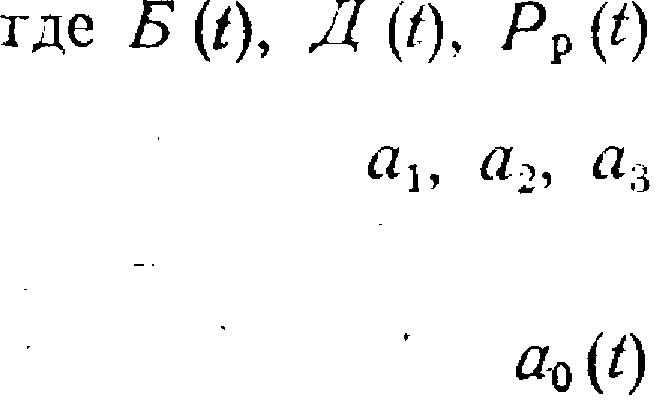
Чаще всего при этом имеют дело с вероятностными и статистическими характеристиками, что обеспечивает возможность количественной оценки качественных категорий объектов.
Основной базой математического аппарата теории надежности являются теория вероятностей и математическая статистика. Следует заметить, что речь идет не о простом применении вероятностно-статистических методов. В теории надежности они имеют свою специфику, требуют специального изучения.
При анализе и расчете надежности технических устройств приходится оперировать случайными величинами. Это обусловлено тем, что отказ любой детали вызывается рядом факторов, большинство из которых имеет случайный характер (качество материала, изготовления и сборки, режимы работы, условия эксплуатации и др.), следовательно, и длительность работы детали до момента отказа будет величиной случайной. Практически очень трудно сохранить постоянство условий производства, однородность исходных материалов и неизменность технологического процесса. Неизбежные колебания всех перечисленных факторов приводят к разбросу качества и свойств готовых изделий. Нельзя предсказать срок службы каждого образца, можно говорить лишь о вероятности того или иного его значения. Все это определяет необходимость использования вероятностно-статистических методов при решении теоретических и практических задач теории надежности.
Теория вероятностей есть математическая наука, изучающая закономерности случайных явлений п распределения случайных величин. Она является не только вычислительным аппаратом теории надежности, но и ее методологической базой, так как позволяет наиболее полно описать процессы создания и использования изделий. Когда речь идет о применении методов теории вероятностей в надежности, иногда приходится слышать заявление о том, что эти методы будто бы узаконивают наличие брака и даже аварий в работе. В действительности же речь идет о методах анализа накопленного материала и разработке на этой основе практических мероприятий по максимальному снижению количества отказов и аварий.
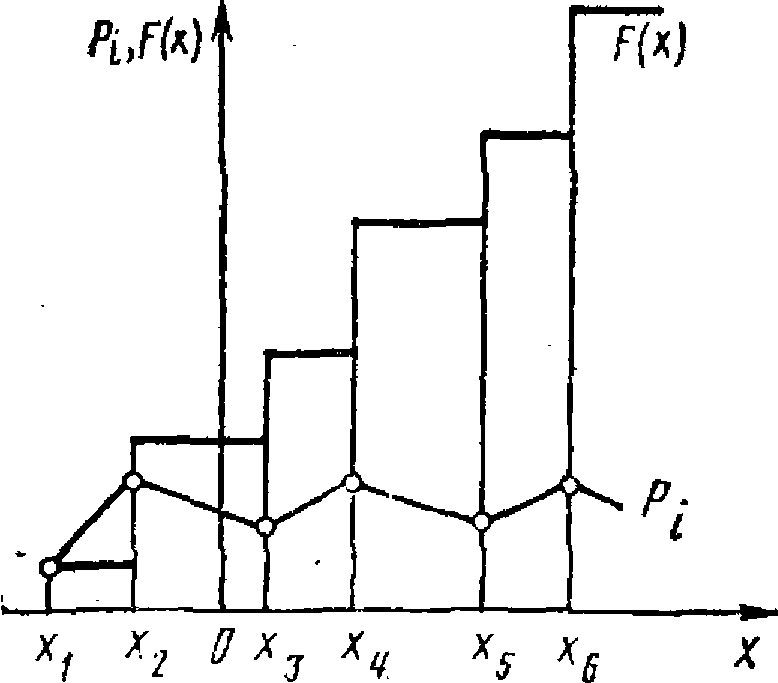
Рис. 1. Многоугольник и функция распределения дискретной случайной величины
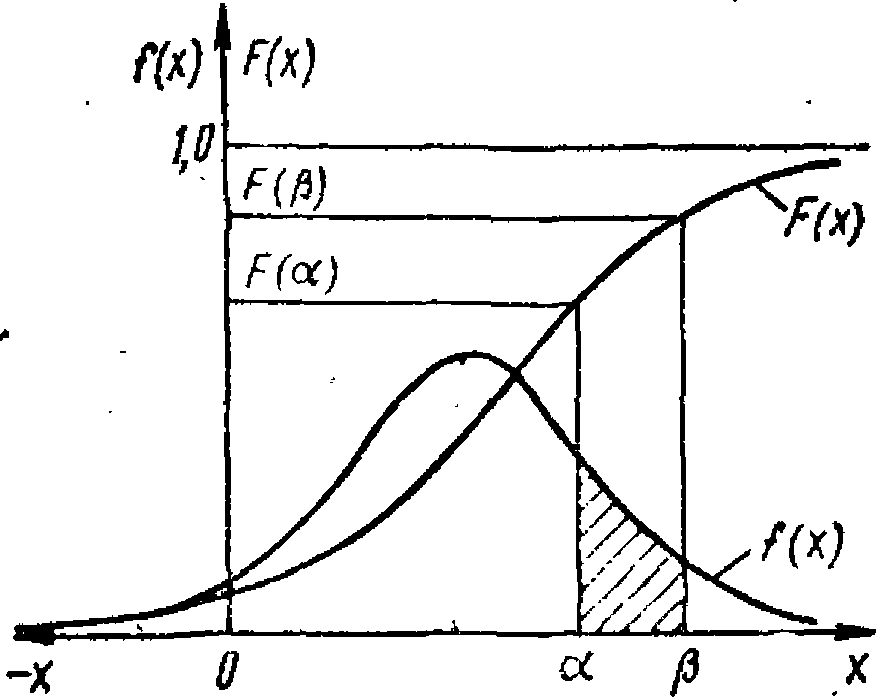
Рис. 2. Плотность вероятностей f(x) и функция распределения F(x) непрерывной случайной величины
В теории надежности используются такие основные понятия, как событие, вероятность, сумма и произведение событий, случайные величины. Многие положения и выводы надежности базируются на применении основных теорем теории вероятностен: о сложении и умножении вероятностей, о повторении опытов, локальной и интегральной теорем Лапласа и др. [1, 2, 3]. На основе формул Бернулли, Лапласа, Пуассона и др. составлены таблицы по расчету надежности [4, 5].
Большое внимание в теории надежности уделяется использованию законов распределения случайных величин, т. е. таких величин, которые в результате опыта могут принять ряд возможных значений.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь различные формы.
Рядом распределения дискретной случайной величины X называется таблица, где перечислены возможные значения этой случайной величины
с соответствующими им вероятностями
где
Графическое изображение ряда распределения (рис. 1) называется многоугольником (полигоном) распределения.
Функцией распределения случайной величины X называется функция F(x), выражающая вероятность того, что X примет значение, меньше чем х,
(4)
Функция распределения есть неубывающая функция, обладающая следующими свойствами:
при
Для дискретных случайных величин функция распределения есть разрывная ступенчатая функция, а для непрерывных случайных величин она непрерывна и дифференцируема.
Дисперсия характеризует степень рассеяния случайной величины относительно ее математического ожидания. Для этой же цели часто применяют среднее квадратическое отклонение
(10) и коэффициент вариации
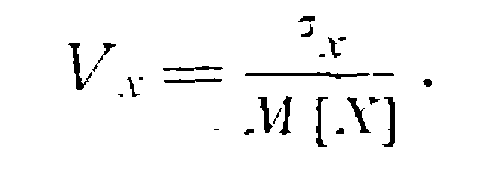(11)
Наиболее часто применяемые законы распределения дискретных и непрерывных случайных величин и их числовые параметры приведены в табл. 1.
Математическая статистика разрабатывает методы обработки данных наблюдений или экспериментов с целью получения научно обоснованных выводов о массовых явлениях и процессах. В результате применения таких методов оказывается возможным определить общие вероятностные характеристики наблюдаемых процессов: вероятности, законы распределения, математические ожидания, дисперсии и др. [1, 3, 6].
Располагая определенной конкретной (часто ограниченной по объему) информацией о наработках до отказа группы объектов, можно на основе применения статистических методов сделать более общие выводы относительно показателей надежности всех объектов этого типа, а также о технологии их изготовления. Следует представлять себе, что полученные по результатам наблюдений за группой объектов выводы и оценки отражают случайный состав объектов группы и потому являются приближенными. Применяя методы математической статистики, например выборочный метод, можно наилучшим способом использовать имеющуюся информацию и на основании исследования выборочной совокупности или выборки из генеральной совокупности получить достаточно достоверные оценки показателей, указывая и степень достоверности. В этом и заключается научная ценность статистических методов и их практическая значимость.
Понятия о выборке и ее характеристиках являются одним из главных в математической статистике. Если имеется некоторая генеральная совокупность случайной величины X, причем эта величина следует закону распределения F(x), то говорят, что генеральная совокупность распределена по закону F(x).
Выполним случайным и независимым образом отбор п значений величины Х из генеральной совокупности и получим некоторую выборочную последовательность x1, x2, ..., xn которая является совокупностью η одинаково распределенных независимых величин X1, X2, ..., Xn. В этом случае считается, что выборка взята из генеральной совокупности величины X. Генеральная совокупность в общем случае может быть и бесконечно большой по объему N (т. е. по числу объектов или признаков), и конечной. Чем больше объем п выборки, тем более обоснованное суждение можно высказать о свойствах генеральной совокупности.
Пусть на оси X взята некоторая точка х, пх — число значений выборки, расположенных левее х, п — общее число значений X в выборке (объем). Тогда отношение
есть частость значений Х<х и зависит функционально от х. Обозначим эту частость Wn(x) и назовем ее функцией распределения выборки или эмпирической функцией распределения
(12)
Wn(x) является оценкой вероятности неравенства Х<х, а следовательно, и оценкой теоретической функции распределения F(x) =Р(Х<х) величины X, т. е. функции распределения генеральной совокупности. Для распределения выборки можно получить выборочные характеристики, которые будут являться оценками параметров характеристик (математического ожидания, дисперсии, асимметрии и др.) теоретического распределения.
Полученные точечные значения оценок могут отличаться от оцениваемых параметров при малом объеме выборки, поэтому пользуются доверительным интервалом, который покрывает неизвестный оцениваемый параметр с заданной вероятностью β. С помощью методов математической статистики, в теории надежности решают большой круг задач, связанных с обработкой данных эксплуатационных наблюдений, обобщениями, прогнозами, проверками гипотез, расчетом показателей надежности и др.