Процесс взаимодействия ведущего колеса и рельса при создании силы тяги очень сложен и его протекание зависит от множества переменных факторов. Взаимодействие зависит от величин нагрузок, передаваемых на рельс колесом: вертикальной силы нажатия и вращающего момента, а также от скорости движения, упругих свойств материалов колеса и рельса, состояния и износа их рабочих поверхностей и ряда других, в том числе и случайных, условий и обстоятельств.
Изучением физических основ сцепления колес с рельсами в течение длительного времени, особенно во второй половине XX столетия занимались многие отечественные и зарубежные ученые и специалисты (только в недавние годы в нашей стране опубликовали свои труды по исследованию вопросов сцепления профессора, доктора технических наук И.П. Исаев, А. Л. Лисицын, А. Л. Голубенко, Ю.М. Лужнов, кандидат технических наук А.Н. Долганов и другие специалисты), и, тем не менее, нельзя сказать, что абсолютная истина в познании этого процесса была достигнута. Существуют различные теоретические гипотезы физического взаимодействия колеса и рельса, которые не могут быть в полной мере экспериментально проверены.
Как уже неоднократно подчеркивалось выше, основным физическим фактором, обеспечивающим возможность поступательного движения ведущего колеса любого колесного транспортного средства, является трение между колесом и дорогой. Трение с точки зрения физики складывается из целого комплекса различных физико-механических процессов, протекающих в поверхностных слоях контактирующих теп.
Различают два основных вида взаимодействия при трении: механическое и молекулярное. Механическое взаимодействие характеризуется взаимным проникновением контактирующих точек вследствие деформации теп при высоких удельных давлениях. Молекулярное взаимодействие связано с взаимным притяжением контактирующих твердых тел, вызываемым неуравновешенным состоянием атомов на их поверхностях. Количественные соотношения между двумя факторами контактного взаимодействия, с одной стороны, ни теоретически, ни экспериментально не определены, но, очевидно, с другой стороны, они могут зависеть от условий и особенностей контакта.
Такой двойственный молекулярно-механический принцип обычно и принимают в качестве «обобщенной» теории трения.
Сложность проблемы контакта колеса и рельса вообще, а при создании силы тяги особенно, делает необходимым рассмотреть ее в упрощенно-популярном, доступном д ля первоначального понимания, представлении, которое, однако, точно соответствует реальным физическим процессам.
При рассмотрении физической природы сцепления будем придерживаться, в основном, позиций популярных объяснений профессоров А.М. Бабичкова (МЭМИИТ) и И.П. Исаева (МИИТ), принятых в их фундаментальных учебниках, ставших уже классическими.
Рабочие поверхности колеса подвижного состава и железнодорожного рельса (рис. 2) в зоне контакта между ними являются цилиндрическими, так как средняя часть стандартного профиля головки отечественных рельсов очерчена по радиусу (r = 300 мм), а коническую поверхность катания колеса, радиус круга катания R которого для стандартных колес локомотивов имеет величину R = 525 мм, если диаметр колес 1050 мм, или R = 625 мм (при диаметре — 1250 мм), в зоне контакта с рельсом можно посчитать так же за цилиндрическую, так как образующие конусной поверхности бандажа при качении перпендикулярны вертикальной оси рельса из-за установки его подошвы с уклоном 1:20 (подуклонки). Контакт двух прижатых друг к другу цилиндров с перпендикулярными осями (z и у) осуществляется в точке, если цилиндры абсолютно жесткие, то есть недеформируемые.
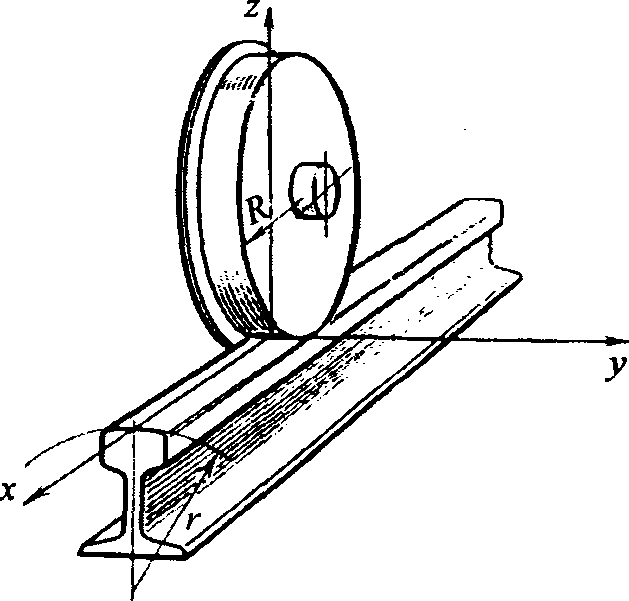
Рис. 2. Качение колеса по рельсу
Из этого исходили выше в п. 1 при рассмотрении процесса создания силы тяги.
В действительности же при контакте под нагрузкой оба тела — колесо и рельс — деформируются. В курсе сопротивления материалов задачи определения деформаций и напряжений при таких взаимодействиях называются контактными.
В основе их решения лежит уравнение известного ученого Г. Герца, полученное им для распределения давлений и напряжений на поверхности гладких упругих тел при их статическом сжатии.
Процесс взаимодействия ведущего колеса и рельса и создания силы сцепления между ними можно представить схематически следующим образом.
В статическом состоянии, ввиду того, что и колесо и рельс не являются абсолютно жесткими и вследствие их деформации под действием вертикальной нагрузки вместо точки контакта А, подразумевавшейся на рис. 1 при абсолютно жестких колесе и рельсе, образуется контактная площадка (рис. 3). Механические свойства материала (стали) контактирующих тел (колеса и рельса) приблизительно одинаковы, но вследствие различия радиусов контактирующих цилиндров контактная площадка двух цилиндров теоретически имеет форму не круга, а эллипса.
В зоне этой площадки вследствие упругих деформаций колеса и рельса имеют место вертикальные напряжения сжатия в колесе и горизонтальные напряжения растяжения на поверхности рельса, распределение которых может быть проанализировано на основе уравнения Герца. По границам (по контуру) площадки напряжения сжатия равны нулю, то есть отсутствуют.

Рис. 3. Схема контакта и упругих деформаций колеса и рельса при статическом нагружении: 1 — эпюра нормальных давлений р в колесе; 2 — то же в рельсе
Примерные формы эпюр нормальных давлений р и напряжений сжатия σ в контактной площадке колеса и рельса при статическом нагружении имеют вид параболических кривых. Они показаны на рис. 3: линия 1 показывает распределение нормальных давлений и напряжений сжатия на поверхности колеса, линия 2 — на поверхности рельса.
Величина контактной площадки между колесом локомотива и рельсом имеет порядок (по площади) 300 — 400 мм2. Именно через такие небольшие по величине площади передаются на рельсы нагрузки от колес подвижного состава, которые на отечественных железных дорогах могут достигать значений П = 125 кН. При этом средние по площади величины напряжений сжатия в колесе и рельсе составляют 300—400 МПа, что превышает величину предела упругости стали.
Наибольшая величина нормального напряжения сжатия σмакс А, естественно, имеет место в центре контактной площадки, где величина вертикальных деформаций колеса и рельса наибольшая. Теоретически она в полтора раза выше среднего напряжения по площадке. И, следовательно, даже при статическом контакте колеса и рельса в их материалах возникают не только упругие, но и пластические остаточные деформации, которые приводят к их постепенному износу.
В момент начала движения (при трогании локомотива с места) после приложения к колесу вращающего момента по площади контактной площадки под действием силы тяги возникают тангенциальные упругие деформации и соответствующие им напряжения сдвига τ (рис. 4).
Причем эти напряжения возникают не на всей площади эллипса, так как передняя его часть (по ходу движения) связана с упругой деформацией волокон колеса и рельса, где трение практически отсутствует (μ = 0 и τ = 0). При этом волокна металла в передней по движению части колеса перед контактной площадкой (зона 1) сжимаются от упора в рельс и вступают в пределы контактной площадки в состоянии упругого сжатия.
То же в этой зоне площадки происходит и с волокнами металла на поверхности рельса
Далее, в начале зоны II (справа на рис. 4), величины коэффициента трения μ и соответственно касательных напряжений, зависящих от деформаций, линейно растут пропорционально возрастающему смещению. К концу зоны II (слева) коэффициент трения достигает своего наибольшего значения. Далее, в пределах зоны III, он остается неизменным по величине (μ = const).
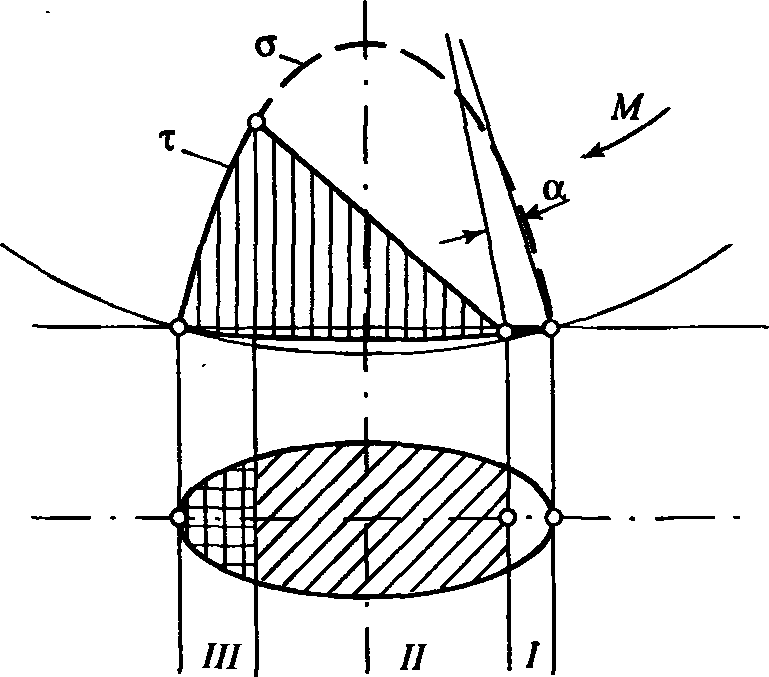
Рис. Распределение касательных напряжений в контактной площадке упруго деформированных колеса и рельса при реализации силы тяги под действием вращающего момента М\ а — угол упругой деформации колеса; σ — эпюра нормальных напряжений в колесе (штриховая линия); т — эпюра касательных напряжений (сплошная линия)
Величина же касательных напряжений τ к границе площадки снижается вследствие уменьшения величины нормальных напряжений σ (по эпюре), так как τ=σμ. Необходимо иметь в виду, что при действии на колесо вращающего момента симметричность распределения напряжений сжатия σ в пределах контактного эллипса искажается. Центр нагрузки несколько смещается в сторону точки упора колеса в рельс, то есть вперед по качению колеса (вправо на рис. 4).
Таким образом, вся контактная площадка между колесом и рельсом в целом как бы делится на две различные части: I — зона чистого качения, в которой практически не действуют силы трения, II и III — зоны сцепления, где взаимодействие колеса и рельса определяется трением.
Волокна поверхности рельса в пределах контактной площадки еще более растягиваются под действием касательной силы от колеса.
В процессе перекатывания колеса перемещается с ним и контактная площадка. При этом сжатые в передней части площадки волокна колеса начинают восстанавливать свою форму, то есть вследствие упругости материала постепенно разжимаются. Одновременно растянутые волокна на поверхности рельса вследствие своей упругости также стремятся восстановить форму, то есть вернуть свое прежнее нерастянутое состояние.
Очевидно, что при этом в пределах контактной площадки неизбежно происходит относительно смещение (упругое проскальзывание) растягивающихся (ранее сжатых) волокон колеса и сжимающихся (прежде растянутых) волокон материала рельса.
Таким образом, в передней части контактной площадки благодаря упругости деформаций имеет место качение колеса без относительного смещения поверхностей колеса и рельса. А в задней по ходу движения части контактной площадки происходит упругое смещение (проскальзывание) поверхностных волокон колеса и рельса относительно друг друга с какой-то скоростью vCK.
В этой стадии приложенная к колесу сила, вызванная моментом, уравновешивается силой трения Fcц, которая по величине находится в пределах от нуля до предельной величины силы трения (сцепления) при отсутствии скольжения — силы трения покоя Fмакс = Пμ0, где μ0 — коэффициент трения покоя.
При дальнейшем увеличении момента и действующей от колеса на рельс силы величина деформаций (растяжения и сжатия) волокон на поверхности колеса и рельса увеличивается и упругое их смещение переходит в относительное проскальзывание, при котором величина силы трения (при движении) уменьшается по сравнению с силой трения покоя и уменьшается сила сцепления между колесом и рельсом. Сцепление колеса и рельса нарушается, оно сопровождается относительным проскальзыванием колеса.
Чем больше скорость движения, тем быстрее сменяются точки поверхности колеса, попадающие в область контактной площадки, тем быстрее протекают процессы упругих деформаций волокон поверхности катания колеса, что связано с увеличением скорости относительного скольжения vCK колеса по рельсу.
Таким образом, создание и реализация силы тяги на основе сцепления колеса и рельса всегда сопровождаются большим или меньшим относительным упругим проскальзыванием колес. Чем больше величина реализуемой силы тяги, тем больше величина относительного проскальзывания.
Именно это проскальзывание и является одной из причин износа поверхности катания ведущих колес и рабочей поверхности рельсов.
При увеличении скольжения может наступить потеря сцепления — боксование.
Действительный характер протекания процессов в зонах контакта ведущих колес локомотивов с рельсами значительно усложняется многими обстоятельствами.
Конусность профиля поверхности катания бандажей и наклонная установка рельсов несколько меняют величины и направления действующих в зоне контакта сил. Значительное влияние оказывают отклонения от начальной формы поперечных профилей колеса и рельса, возникающие вследствие их износа. Из-за проката бандажей форма, расположение и размеры контактной площадки меняются. По мере роста проката полуоси контактного эллипса становятся близкими друг к другу по величине, его форма приближается к прямоугольнику, и, более того, при существенном износе бандажей большая ось площадки может изменить ориентацию и стать направленной не вдоль, а поперек продольной оси рельса.
Существенное влияние на процесс взаимного контакта колес и рельсов оказывает наличие так называемой «третьей фазы» — посторонних веществ — между колесами и рельсами (пыль, грязь, листья и другие остатки растительности, следы смазочных материалов и атмосферные осадки и явления — дождь, снег, иней, лед), которые, играя роль своего рода смазки, могут заметно снижать величину коэффициента трения между ними.
Но это отличия количественные. Изучать и оценивать подробные детали и особенности этого процесса бывает необходимо лишь со специальными целями.
На данном этапе первоначального знакомства с теорией локомотивной тяги для понимания и изучения дальнейших вопросов этой теории и для выполнения тяговых расчетов вполне достаточно изложенного выше упрощенного качественного представления процесса сцепления колеса с рельсом.
Различные понятия о силе тяги и мощности локомотивов. Выше, в п. 2.1, было показано, что силу тяги локомотивов FK на железнодорожном транспорте принято относить к точкам касания колес и рельсов. В связи с этим необходимо различать и понятия о мощности локомотивов.
В локомотивостроительной промышленности и на железнодорожном транспорте СССР за мощность тепловозов принимали номинальную величину эффективной мощности дизеля Ne секции тепловоза (или тепловоза в целом). Для электровозов за мощность локомотива принимают суммарную электрическую мощность, потребляемую тяговыми электродвигателями.
Очевидно, что действительная мощность локомотива, используемая для движения поезда и развиваемая на ведущих колесах локомотива, N в любом случае меньше указанных выше величин.
Для тепловозов NK = Ne (1 - β) ηпеρ, где β — доля мощности дизеля, затрачиваемая на привод вспомогательного оборудования тепловоза; ηпеρ — коэффициент полезного действия передачи тепловоза.
Величину мощности Νκ, по аналогии с касательной силой тяги FK, называют касательной мощностью локомотива.
Иногда выделяют так называемую полезную силу тяги локомотива Fn — на сцепке (или на крюке, как называли раньше, до появления автосцепки) — то есть ту часть силы тяги FK, которая затрачивается непосредственно на движение состава вагонов (за вычетом затраты силы на движение самого локомотива).
При равномерном движении Fn = FK- W, где W — сила сопротивления движению локомотива.
В некоторых системах тяговых расчетов тяговые возможности локомотивов оцениваются именно по величине силы тяги на сцепке.
