Основные физические понятия и величины, относящиеся к механике транспортного движения, их обозначения и единицы измерения. В расчетах, связанных с определением параметров движения поездов и работы локомотивов, используются известные из физики общие основные законы, понятия и величины, относящиеся к следующим ее разделам: механика (кинематика, статика и динамика); термодинамика и общая электротехника.
Эти понятия, законы и величины вводятся еще при изучении начального (общего) курса локомотивов. Но, тем не менее, необходимо здесь их кратко напомнить и привести наиболее распространенные обозначения и единицы измерения применяемых на транспорте физических величин и используемых в дальнейшем в данном учебнике.
МЕХАНИКА.
В любом одномерном поступательном движении координатами движущегося тела являются следующие величины.
- Путь (длина пройденного в движении пути, расстояние от начальной точки, начала координат) S, км.
Отрезок пути ∆S определяется как разность значений пройденного пути в начальной (1) и конечной (2) точках, а именно:
![]()
Все расстояния в транспортном движении обычно (за малыми исключениями) измеряются в километрах, км.
- Время в пути (время движения) t, мин.
Отрезок (промежуток) времени ∆t определяется как
![]()
Время в расчетах, связанных с движением поездов, как правило, измеряют в минутах, мин.
Полезно вообще иметь в виду, что вопрос о выборе рациональных единиц измерения в различных отраслях науки и техники имеет существенное практическое значение. Системы единиц измерения, в том числе и Международная (СИ), строятся исходя из так называемых основных и производных единиц, которые далеко не всегда в конкретных ситуациях удобны для использования. Поэтому и используются кратные и дольные единицы физических величин.
При любых измерениях и подсчетах физических величин обычно единицы измерения стремятся выбирать так, чтобы численные значения этих величин находились бы в диапазоне от единиц до сотен, то есть имели бы от одной до, по возможности, не более чем трех значащих цифр. С такими величинами легче обращаться, в такой форме их легче запоминать. Именно поэтому линейные размеры машин в технике, а особенно их деталей, измеряют в миллиметрах, портные же в своей работе пользуются сантиметрами (так как в сантиметрах любой размер человеческого тела выражается не более чем тремя цифрами), а строители и землемеры — метрами. Для железнодорожных транспортных расстояний наиболее удобен в качестве единицы измерения длины километр, так как длины перегонов, участков, маршрутов и
линий чаще всего имеют порядок от единиц до сотен километров, и, даже в нашей большой стране, лишь в отдельных случаях железнодорожные расстояния могут превышать тысячу километров.
Точно так же и со временем. Для измерения времени хода, составления расписаний движения поездов представление времени в минутах наиболее удобно: секунда слишком малая, а час—слишком крупная для этого единица. Одинаково неудобно, например, сказать или услышать, что какая-то поездка продолжалась «1500 секунд» или «0,413 часа», тогда как «25 минут»—всем привычны и понятны, легко воспринимаются и запоминаются.
КИНЕМАТИКА.
Путь и время, по сути дела, даже не параметры движения, характеризующие его кинематику, а просто координаты движущегося тела по осям расстояния и времени его движения. Следующие две величины уже непосредственно являются кинематическими параметрами движения.
- Скорость движения v (малая, строчная буква), км/ч.
Скорость: по физическому определению—это расстояние, проходимое в единицу времени (при равномерном, то есть с неизменной постоянной скоростью, движении); математически же это—производная текущего значения пройденного пути (то есть расстояния) по времени.
Соответственно поэтому можно иметь два разных представления о скорости движения.
Строго говоря, v=dS/dt — это «мгновенная» скорость, скорость в данный момент времени. Чтобы ее можно было определить как производную, надо знать непрерывную функцию S=f(t), чтобы иметь возможность ее продифференцировать. Но эта функция как раз и является чаще всего искомой в расчетах по движению поезда.
Зная ее, можно было бы путем интегрирования уравнения dS = vdt получить зависимость расстояния от времени, что вообще-то и является одной из цепей таких расчетов.
Но все дело в том, что до начала расчетов эта функция неизвестна. Поэтому пользоваться понятием мгновенной скорости для расчетов транспортного движения не только просто неудобно, да и не имеет смысла. Мгновенное значение скорости — это та величина, например, на которую показывает стрелка спидометра на автомобиле при его движении, она постоянно колеблется в ту или иную сторону даже при относительно установившемся режиме движения.
В тяговых расчетах обычно пользуются понятием средней скорости движения vcp при движении на расстоянии![]() за промежуток времени
за промежуток времени![]()
Она по определению равна:
![]() (1.1)
(1.1)
Скорость поступательного транспортного движения принято и привычно измерять числом километров пути, пройденного за час времени движения, то есть в километрах в час [км/ч]. Поэтому в формулу (1.1) время надо подставлять в часах, либо в отличие от ее общего вида, применяемого в физике, для использования в тяговых расчетах надо вставить в нее множитель 60, так как мы договорились время измерять в минутах, а именно:
![]() (1.2)
(1.2)
где (S2 - S1) в км, а (t1-2 ) в мин.
В дальнейшем под скоростью v мы чаще будем подразумевать именно среднюю скорость движения за какой-то промежуток времени. Поэтому индекс «ср» у обозначения скорости можно и не писать, подразумевая, что ν это и есть ν/ср.
Как видим, ошибка оказалась не так уж велика, но все же ее относительная величина составила 4 %, и, вдобавок, это была принципиальная ошибка, недопустимая для образованного человека, а тем более специалиста.
4. Ускорение а.
Ускорение — это «скорость изменения скорости», то есть производная скорости по времени или вторая производная пути по времени.
![]() — это мгновенное ускорение, ускорение в данный
— это мгновенное ускорение, ускорение в данный
момент времени.
По причинам, изложенным выше применительно к скорости, может использоваться и понятие среднего ускорения:
![]()
Однако надо иметь в виду, что величина среднего ускорения за какой- то промежуток времени имеет смысл лишь для монотонного процесса изменения скорости во времени (увеличения или уменьшения ее).
Единицы измерения ускорения могут быть разными: км/ч2, км/ч · мин и км/ч · с. Чаще применяется наиболее удобная вторая форма единицы измерения: «километры в час за минуту», то есть изменение скорости на один километр в час за одну минуту.
СТАТИКА И ДИНАМИКА.
Эти разделы механики связаны с действием сил. Поэтому здесь надо ввести понятия основных сил, действующих на поезд при его движении.
1. Вес (сила тяжести), кН.
Для разных объектов железнодорожного движения вес обычно обозначается по-разному:
-вес локомотива — Р;
-вес состава вагонов — Q;
-вес поезда — (P+Q),
-вес вагона — q.
Вес всех единиц подвижного состава измеряется в единицах силы. Принято использовать наиболее удобную по величине единицу — «килоньютон» (кН).
В технической и учебной литературе прежних лет издания и, в частности, в «Правилах тяговых расчетов для поездной работы» издания 1985 г., для измерения сил (в формулах и графических характеристиках) использованы внесистемные единицы так называемой «практической» системы — «килограмм-сила», или кгс. Пользуясь в расчетах данными этих литературных источников, можно приблизительно считать, что 1 кгс = 10 Н (точное соотношение 1:9,81, где 9,81 м/с2=g — ускорение силы тяжести). Неточность, связанная с этим округлением, вполне допустима, так как составляет всего 1,9 %, то есть лежит в пределах погрешностей любых технических расчетов, зато позволяет избежать как пересчетов, так и получения в результатах при механическом умножении или делении числовых величин с большим количеством псевдозначащих цифр.
Не следует смешивать или путать и понятия массы и веса, чему ранее при практической системе единиц часто не придавалось значения из-за однотипности единиц измерения.
Вес — это вертикальная сила, сила тяжести, и о нем приходится говорить, когда речь идет о силе воздействия, например, подвижного состава на железнодорожный путь.
Масса — скалярная величина, которая используется как мера количества вещества или инертности тела. Для отдельных единиц подвижного состава и поезда в целом масса измеряется не в килограммах — основной единице, принятой в СИ, а в более крупных единицах—тоннах, т. Для массы введем такие обозначения:
-масса локомотива — Мр,
- масса состава — Mq,
-масса поезда — M=Mp+Mq,
-масса вагона — т.
- Нагрузки от оси (колесной пары) подвижного состава на рельсы, кН:
-локомотива — 2П;
-вагона — q0.
2П = Pln и q0 = qln, где п — число осей (колесных пар) соответственно локомотива и вагона.
- Горизонтальные силы, которые обычно по своей величине на порядок меньше вертикальных сил тяжести (веса) в железнодорожной практике измеряются в основных единицах силы — ньютонах, Н. Обозначаются они так:
-сила тяги — FK;
-сила сопротивления движению— WK;
-тормозная сила — Вт.
Значения подстрочных индексов при обозначении горизонтальных сил будут объяснены в последующем.
- Удельные горизонтальные силы представляют собой отношения соответствующих сил к общему весу всего поезда (P + Q), а именно:
- удельная сила тяги fK = FKl(P+Q); (1.3)
- удельная сила сопротивления wк = W (P+Q); (1.4)
-удельная тормозная сила bТ=Вт/(Ρ+ Q ); (1.5)
По определению удельные силы не имеют размерности (сила делится на силу), но в связи с принятыми выше различными единицами измерения вертикальных сил (веса) и горизонтальных сил, действующих на поезд, получаем для удельных горизонтальных сил условную составную единицу измерения—Н/кН или %о, то есть «промилле» (тысячные доли).
Геометрические характеристики железнодорожного пути.
Перечень условных обозначений и единиц измерения физических величин, связанных с описанием движения поезда, необходимо дополнить конкретными геометрическими характеристиками участка железнодорожного пути, по которому осуществляется движение поезда. Это, в первую очередь, длины его элементов:
-длины участков пути, перегона, элементов продольного профиля участка пути — l, км;
- полезная длина станционных путей — lст, м.
На большой части железнодорожных линий России полезная длина приемо-отправочных путей станций (используемая для размещения поезда) составляет 1050 или 850 м. На линиях, подготовленных для обращения тяжеловесных и длинносоставных поездов, длина отдельных путей станций может составлять 1250 и 1700 м. На некоторых второстепенных участках могут сохраняться станции с длиной путей 720 м, которая была распространена ранее;
- длина криволинейного участка пути (длина кривой) — Sкр, м;
- радиус кривизны участка пути в плане (радиус кривой) — R, м;
- уклон элемента продольного профиля пути — i, %о.
Линейные размеры подвижного состава:
- длина локомотива — lл, м;
- длина вагона — lв, м;
- длина поезда — lп, м. lп = lл + Σ lв.
Помимо обозначений и единиц измерения напомним и основные законы (или аксиомы) механики, которые известны из физики как законы Ньютона:
- Тело (изолированная материальная точка) при отсутствии внешних сил (или при равенстве нулю их суммы) сохраняет состояние покоя или прямолинейного равномерного движения.
- Ускорение материальной точки прямо пропорционально действующей на нее силе и обратно пропорционально ее массе.
- Действие равно противодействию.
Эта законы механики дополняются законом параллелограмма о сложении сил: «Если на материальную точку действуют две силы, то она движется так, как если бы была одна сила, являющаяся геометрической суммой двух действующих сил».
Транспортное движение в пространстве
Транспортное движение в пространстве в общем случае, как уже указывалось, является трехмерным. В его процессе могут меняться во времени все три геометрические координаты транспортного средства.
Для водного (надводного, но не подводного) транспорта движение судов, очевидно, является двухмерным, то есть движением на плоскости, за которую обычно принимается поверхность Мирового океана. С некоторыми оговорками (о которых речь будет идти ниже) двухмерным можно посчитать и движение наземного транспорта.
Для железнодорожного транспорта с некоторыми условностями, упрощающими анализ, движение подвижного состава, направляемое рельсовым путем по его оси, можно рассматривать даже как одномерное.
Рассмотрим простейшие частные случаи одномерного прямолинейного транспортного движения.
Движение но горизонтальной поверхности.
В учебниках физики всегда рассматривается простейший пример прямолинейного движения тела по горизонтальной плоскости.
Тело (предмет) А лежит (рис. 1.3, а) на горизонтальной опорной поверхности Б (или плавает на поверхности жидкости). Сила тяжести (вес) тела Р = mg действует на опорную поверхность сверху вниз. Реакция опорной поверхности N (или выталкивающая сила жидкости) по закону равенства действия и противодействия равна силе тяжести по величине и противоположна по направлению.
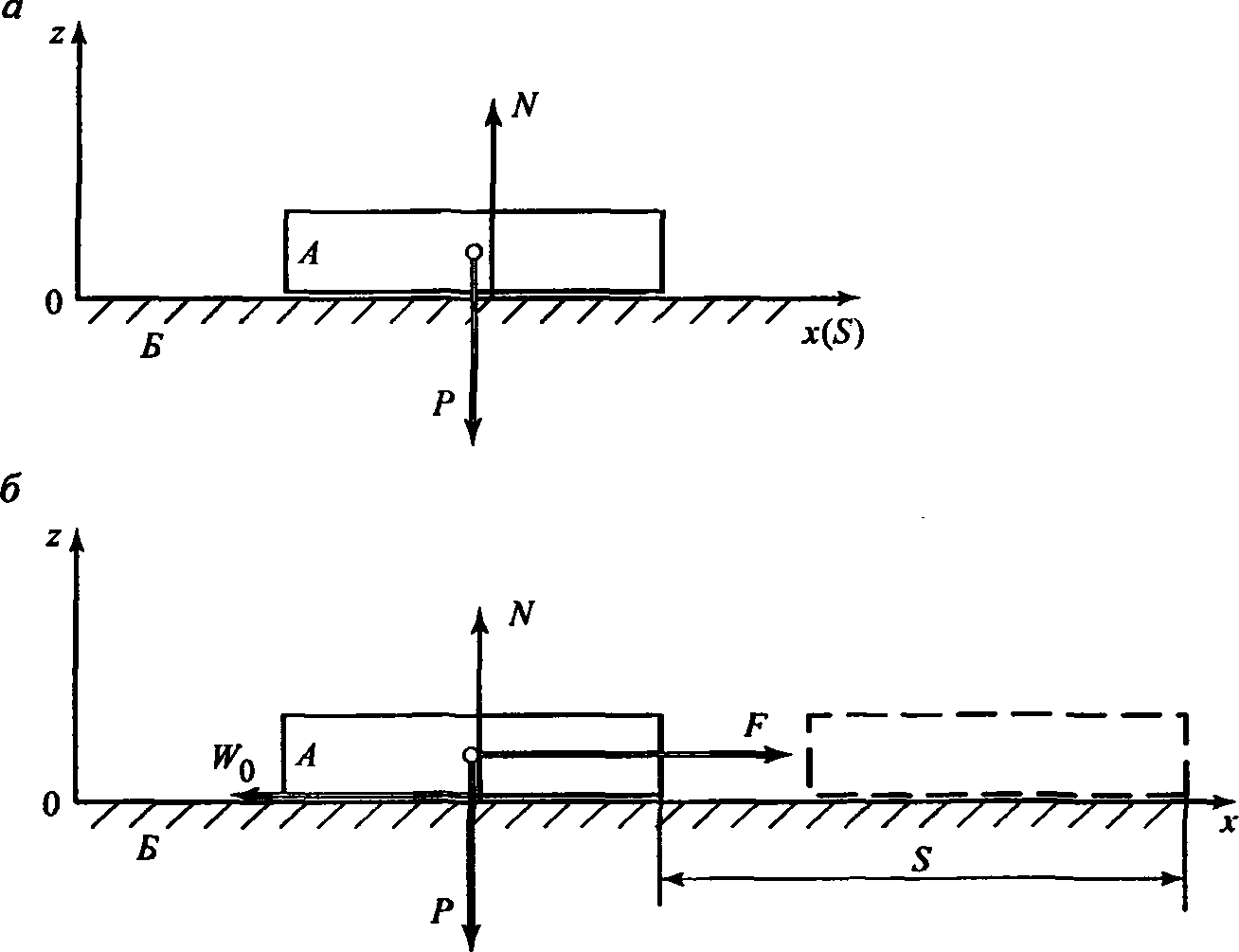
Рис. 1.3. Силы, действующие на тело на горизонтальной поверхности: а — в состоянии покоя; 6 — в состоянии движения
Вследствие равенства величин и противоположности направлений сип, действующих на тело по вертикальной оси z, их сумма или равнодействующая равна нулю: тело находится в состоянии покоя. Поэтому по оси z никакого движения вообще быть не может (движение вниз ограничено опорной поверхностью, а вверх оно невозможно, так как сила реакции равна весу тела (N = Р) по третьему закону Ньютона всегда, и быть больше веса Р не может).
Таким образом, прямолинейное движение тепа в этих условиях в принципе возможно только по горизонтальной оси х (5), то есть может быть одномерным.
Тело А можно вывести из состояния покоя и привести его в движение по горизонтали, если приложить к нему внешнюю силу, направленную в сторону движения, например вправо. Потянем тело А вправо с силой F, например, при помощи гибкой нити (рис. 1.3,6).
Если сила F превысит по величине силу трения покоя между телом и поверхностью, то тело сдвинется с места и начнет перемещаться вправо. После начала движения препятствовать ему будет сила сопротивления движению W0, то есть в данном случае сила трения скольжения между предметом и поверхностью. По закону Кулона — Амонтона величина силы трения при скольжении прямо пропорциональна величине силы нормального давления, то есть силе тяжести Р, а именно W0 = Ρμ, где μ — коэффициент трения. В данном случае, это коэффициент трения скольжения, величина которого зависит от материалов и состояния трущихся поверхностей. В дальнейшем, если величина силы F будет продолжать оставаться больше W0 , равнодействующая этих сил, действующих на тело по горизонтали, будет направлена вправо, и движение тела будет ускоренным. Величина ускорения а тела по второму закону Ньютона прямо пропорциональна величине равнодействующей силы R= F-W0 и обратно пропорциональна массе т тела: а=(F-W0)/т.
Таким образом, движение тела по горизонтальной поверхности связано с наличием двух групп сил. Две вертикальные силы (тяжести и нормальная реакция опорной поверхности или пути) уравновешены. Поэтому движение и горизонтально: силой тяжести тело прижато к поверхности пути.
Две горизонтальные силы в общем случае не уравновешены. Сила сопротивления движению W0 появляется с момента начала движения, она объективна и не управляема. Ее величина не зависит от того, кто организует движение.
Величина силы полностью зависит от возможностей транспортного средства и определяется тем, кто им управляет. От ее величины и зависит характер движения. Поэтому силу F и называют движущей силой или силой тяги (в колесном транспорте).
Чтобы движение могло продолжаться, по крайней мере, необходимо соблюдать условие F= W0, что по первому закону механики может быть условием равномерного движения по линии действия этих сил.
Если F= W0 , то F= Рμ.
Разделим оба равенства почленно на вес тела Р и получим равенства удельных сил тяги и сопротивления:
![]() (1.6)
(1.6)
И, следовательно, для возможности движения, как минимум, должно иметь место последнее равенство, обеспечивающее возможность равномерного движения физического тела.
Таким образом, возможность движения вообще всегда связана с необходимостью преодоления сил трения, которые являются силами сопротивления движению.
Перемещение тела на расстояние S по горизонтали (см. рис. 1.3, б) под действием приложенной к нему силы F связано с совершением механической работы A=FS.
Силы сопротивления движению.
Сопротивление движению на рассмотренных простейших схемах (см. рис. 1.3) — это сила трения скольжения, которая зависит от величины коэффициента трения, который, в свою очередь, зависит от материалов, шероховатости и состояния трущихся поверхностей, наличия и вязкости смазки между ними, скорости относительного перемещения и т.п.
Для трения дерева по дереву величина коэффициента трения скольжения имеет порядок μ = 0,3, металла по металлу — μ = 0,2. Для скольжения твердых поверхностей со смазкой μ лежит примерно в пределах 0,05 — 0,10.
Таким образом, для перемещения тела «волоком» по горизонтальной поверхности необходимо тянуть его с силой, равной по величине примерно 20 % его веса. Это легче, чем поднимать груз, и поэтому, когда груз было трудно поднимать, наши предки волочили его по земле. Наличие смазки, например воды, между поверхностями уменьшает силу трения скольжения примерно вдвое, но все равно она оказывается достаточно большой, если иметь в виду массовые перевозки грузов. В таких условиях, если пришлось бы тянуть волоком какой-то груз, серийный тепловоз 2ТЭ116, величина максимальной силы тяги которого при трогании с места имеет порядок 800 кН, смог бы сдвинуть с места груз массой всего только 400—800 т (при собственной массе локомотива 270 т).
Перемещение грузов на колесах значительно снижает силу сопротивления движению. Сипа трения качения может быть в десятки и даже в сотни раз меньше, чем при скольжении. Причем она будет тем меньше, чем жестче (или тверже) колесо и дорога.
Наши рельсовые дороги потому и стали «железными», так как стальные (или чугунные) колеса по стальным рельсам среди других конструкционных материалов имеют минимальный коэффициент трения качения. И тот же тепловоз мог бы вести на колесах (правда, только по прямому и горизонтальному рельсовому пути) состав массой не менее 20000—25000 т.
В малой величине коэффициента трения качения стального колеса по стальному рельсу и состоит основное достоинство железнодорожного транспорта и его экономическое преимущество перед другими видами наземного транспорта. Поэтому, например, перевозка груза по железной дороге требует в несколько раз меньшей затраты энергии по сравнению с автомобильным транспортом.
Движение на наклонной поверхности. Особенностью средств наземного транспорта является то, что наземные дороги не могут быть строго горизонтальными. Переменный рельеф земной поверхности приводит к неизбежности наличия подъемов и спусков на автомобильных и железных дорогах.
Если транспортируемое тело находится на наклонной плоскости (на спуске или подъеме, как показано на рис. 1.4), характер действия сил, действовавших на горизонтальной плоскости, несколько меняется, независимо от вида трения при движении.

Рис. 1.4. Движение тела на наклонной плоскости
Так как ось координат в направлении движения не горизонтальна, а совпадает с наклонной плоскостью, угол наклона которой к горизонтали имеет величину а, то вторая ось координат перпендикулярна плоскости, и именно в этом направлении взаимодействуют при движении транспортное средство и дорога.
Поэтому, прежде всего, разложим силу тяжести Р транспортного средства на две взаимно перпендикулярные составляющие по осям координат, одна из которых направлена вдоль пути, а другая — перпендикулярна пути.
Последняя составляющая — Р cosa — прижимает транспортное средство к пути на подъеме и определяет величину силы трения между ними. Эта сила несколько меньше веса Р, так как cos.a < 1 при любой реальной величине угла наклона пути а.
Первая составляющая силы тяжести — Psin.a — направлена в сторону, противоположную движению на подъем, и, следовательно, является дополнительным сопротивлением движению. Именно поэтому тянуть груз (или поезд) на подъеме значительно труднее, чем по горизонтальному пути. Причем тем труднее, чем больше величина угла наклона а.
Таким образом, суммарная величина силы сопротивления движению транспортного средства W на подъеме равна сумме двух слагаемых: величины основного сопротивления, то есть сопротивления движению по горизонтальному пути, которое, как было показано выше, определяется трением, а именно силой W0=(Р cos.a) μ, и силой дополнительного сопротивления, которая представляет собой составляющую силы тяжести Р sin.a:
![]() (1.7)
(1.7)
Если перейти к удельным силам (разделив все члены равенства на Р), получим:
![]() (1.8)
(1.8)
Величины тригонометрических функций угла наклона а можно выразить через его геометрические параметры: длину l и высоту h подъема. Например, sin.a = hi I.
При проектировании дорог, как автомобильных, так и, тем более, железных, стремятся минимизировать крутизну необходимых подъемов и спусков.
На магистральных железных дорогах углы допускаемых максимальных уклонов обычно не превышают величины 1,15° (Г 090 — при этом sin.a=0,02. При меньших величинах углов наклона (например, 1 °, 0,5° и 0,3°) синусы этих углов соответственно имеют значения 0,0175, 0,0087 и 0,0052. Иными словами, синусы углов наклона пути к горизонтали на железной дороге имеют порядок тысячных долей единицы. Поэтому в качестве параметра, характеризующего крутизну уклонов железнодорожного пути, используется величина синуса угла, увеличенная в 1000 раз. Она называется уклоном i и измеряется именно в тысячных долях (промилле) — %о.
![]() (1.9)
(1.9)
Величину уклона в тысячных просто подсчитать, если принять разные единицы измерения для высоты и длины уклона: длину уклона выражать, как и прежде расстояние, в километрах, а высоту в единицах, в 1000 раз меньших, то есть в метрах:
![]() (1.10)
(1.10)
Уклон в одну тысячную, таким образом, соответствует крутизне участка пути, когда на длине одного километра пути высота увеличивается на один метр.
Отметим, что при малых значениях углов наклона а железнодорожного пути величина косинуса угла очень близка к единице. Если sin.a < 0,020, то cos.a > 0,9998, то есть при любой практически возможной точности расчетов величина косинуса угла наклона элемента продольного профиля железнодорожного пути может и должна считаться равной единице. Тогда, считая cos.a = 1, можно вышеприведенное равенство удельных сил при равномерном движении преобразовать к более простому виду:
![]() (1)
(1)
Последняя форма равенства (1) наглядно показывает, из каких составляющих складывается сопротивление движению на подъеме и от чего оно зависит: от величин коэффициента трения и угла наклона (в данном случае — подъема) пути.
Очевидно, всегда следует иметь в виду, что на спуске направление действия составляющей веса Р sin.a соответствует направлению движения. Она не препятствует, а способствует движению. Дополнительное сопротивление (как мы его назвали) в данном случае уже не является сопротивлением движению. Можно сказать, что оно имеет отрицательную величину и является как бы «отрицательным сопротивлением», так как направление его действия совпадает с направлением движущей силы.
Поэтому для общности условие возможности равномерного движения на уклоне пути следует написать так:
![]() (2)
(2)
Из последнего равенства (2) видно, что условием возможности равномерного движения на спуске является равенство:
![]() (3)
(3)
Из равенства (3) вытекает известное из жизни положение — для движения на спуске требуется меньшая величина движущей силы.
И, более того, если sin.a > μ, то движение может наступить самопроизвольно (например, от случайного порыва ветра), без участия внешней искусственной движущей силы f (то есть при полном ее отсутствии). Поэтому, в частности, на путях станций, имеющих хотя бы очень небольшой уклон, вагоны и составы, стоящие на путях, обязательно фиксируют на рельсах тормозными башмаками.
